

���� ��1����ͼ1�У��ӳ�AD��K��ʹ��DK=AD������AN��KN��KM������֤����ADB�ա�KDM����֤����ANC�ա�KNM���Ƴ���ANK�ǵ���ֱ�������μ��ɽ�����⣮
��2�����ۣ�AD=DN���ӳ�AD��K��ʹ��DK=AD������AN��KN��KM������֤����ADB�ա�KDM����֤����ANC�ա�KNM���Ƴ���ANK�ǵ���ֱ�������μ��ɽ�����⣮
��3�����ۣ�AD=DN��AD��DN���ӳ�AD��K��ʹ��DK=AD������AN��KN��KM������֤����ADB�ա�KDM����֤����ANC�ա�KNM���Ƴ���ANK�ǵ���ֱ�������μ��ɽ�����⣮
��� ��1��֤�����ⷨһ����ͼ1�У��ӳ�AD��K��ʹ��DK=AD������AN��KN��KM��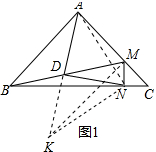
�ڡ�ADB�͡�KDM�У�
$\left\{\begin{array}{l}{AD=DK}\\{��ADB=��KDM}\\{BD=DM}\end{array}\right.$��
���ADB�ա�KDM��
��AB=KM=AC����BAD=��MKD��
��AB��KM��
���KMC=��BAC=90�㣬
��AB=AC����BAC=90�㣬
���C=45�㣬��MN��BC��
���MNC=90�㣬��NMC=45��=��KMC=��C��
��MN=NC��
�ڡ�ANC�͡�KNM�У�
$\left\{\begin{array}{l}{CN=MN}\\{��ACN=��KMN}\\{AC=KM}\end{array}\right.$��
���ANC�ա�KNM��
��AN=KN����ANC=��KNM��
���KNA=��MNC=90��
��AD=DK��
��DN=AD=DK��
��AD=DN��
�ⷨ��������ֱ��������б���������ʣ���֪AD=$\frac{1}{2}$BM��DN=$\frac{1}{2}$BM���ɴ˼���֤����
��2����ͼ2�У����ۣ�AD=DN��
���ɣ��ӳ�AD��K��ʹ��DK=AD������AN��KN��KM��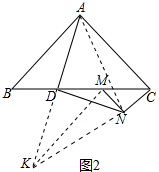
�ڡ�ADB�͡�KDM�У�
$\left\{\begin{array}{l}{AD=DK}\\{��ADB=��KDM}\\{BD=DM}\end{array}\right.$��
���ADB�ա�KDM��
��AB=KM=AC����BAD=��MKD��
��AB��KM��
���KMD=��B=45�㣬
�ߡ�NMC=��NCM=��ACB=45��
��MN=NC����KMN=��ACN=90��
�ڡ�ANC�͡�KNM�У�
$\left\{\begin{array}{l}{CN=MN}\\{��ACN=��KMN}\\{AC=KM}\end{array}\right.$��
���ANC�ա�KNM��
��AN=KN����ANC=��KNM��
���KNA=��MNC=90��
��AD=DK��
��DN=AD=DK��
��AD=DN��
��3����ͼ3�У����ۣ�AD=DN��AD��DN��
���ɣ��ӳ�AD��K��ʹ��DK=AD������AN��KN��KM���ӳ�KN��AC��G��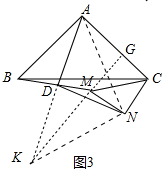
�ڡ�ADB�͡�KDM�У�
$\left\{\begin{array}{l}{AD=DK}\\{��ADB=��KDM}\\{BD=DM}\end{array}\right.$��
���ADB�ա�KDM��
��AB=KM=AC����BAD=��MKD��
��AB��KM��
���KGC=��BAC=90�㣬
���ACN+��NMG=180�㣬
�ߡ�KMN+��NMG=180�㣬
���ACN=��NMK��
�ڡ�ANC�͡�KNM�У�
$\left\{\begin{array}{l}{CN=MN}\\{��ACN=��KMN}\\{AC=KM}\end{array}\right.$��
���ANC�ա�KNM��
��AN=KN����ANC=��KNM��
���KNA=��MNC=90��
��AD=DK��
��DN=AD=DK��DN��AK��
��AD=DN��AD��DN��
���� ���⿼�鼸�α任�ۺ��⡢ȫ�������ε��ж������ʡ�����ֱ�������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬��סͼ�η����仯�����۲��䣬֤���ķ���Ҳ�����Ƶģ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
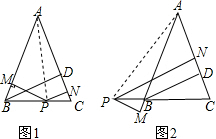 ��ͼ1���ڡ�ABC�У�AB=AC��BD�ǡ�ABC�ĸߣ�P��BC����һ�㣬PN�ֱ���ֱ��AB��AC��ֱ������ֱ�Ϊ��M��N����֤��BD=PM+PN��
��ͼ1���ڡ�ABC�У�AB=AC��BD�ǡ�ABC�ĸߣ�P��BC����һ�㣬PN�ֱ���ֱ��AB��AC��ֱ������ֱ�Ϊ��M��N����֤��BD=PM+PN���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������������A�����һ����¥����B�ĸ���Ϊ23�㣬����ⶰ��¥�ײ�C�ĸ���Ϊ45�㣮��֪������A�������ĸ߶�Ϊ180m�����ⶰ��¥�ĸ߶ȣ���ȷ��1m�������ο����ݣ�sin23��=0.39��cos23��=0.92��tan23��=0.42��
��ͼ������������A�����һ����¥����B�ĸ���Ϊ23�㣬����ⶰ��¥�ײ�C�ĸ���Ϊ45�㣮��֪������A�������ĸ߶�Ϊ180m�����ⶰ��¥�ĸ߶ȣ���ȷ��1m�������ο����ݣ�sin23��=0.39��cos23��=0.92��tan23��=0.42���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
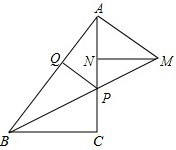 ��ͼ����֪���ڡ�ABC�У���ACB=90�㣬��P���߶�AC��һ�㣬����A��AB�Ĵ��ߣ���BP���ӳ����ڵ�M��MN��AC�ڵ�N��PQ��AB�ڵ�Q��AQ=MN��NP=2��PC=3��
��ͼ����֪���ڡ�ABC�У���ACB=90�㣬��P���߶�AC��һ�㣬����A��AB�Ĵ��ߣ���BP���ӳ����ڵ�M��MN��AC�ڵ�N��PQ��AB�ڵ�Q��AQ=MN��NP=2��PC=3���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com