
【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60°后,得到△AP′C,则∠APC=_____°.
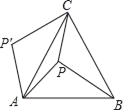
【答案】150°
【解析】
如图,连接PP′,根据旋转的性质证明△APP′是等边三角形,可得∠APP′=60°,PP′=PA=6,再由勾股定理的逆定理判定△P′PC是以∠P′PC为直角的直角三角形,即可求得∠APC的度数.
如图,连接PP′,

∵△APB绕点A逆时针旋转60°得到△AP′C,
∴△AP′C≌△APB,
∴P′A=PA=6,P′C=PB=10,
∵旋转角是60°,
∴△APP′是等边三角形,
∴∠APP′=60°,PP′=PA=6,
∵PP′2+PC2=62+82=100,P′C2=PB2=102=100,
∴PP′2+PC2=P′C2,
∴△P′PC是以∠P′PC为直角的直角三角形,
∴∠APC=∠APP′+∠P′PC=60°+90°=150°.
故答案为:150°.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】根据你的经验,下列事件发生的可能性哪个大哪个小?根据你的想法,把这些事件的序号按发生的可能性从小到大的顺序排列________.
![]() 从装有
从装有![]() 个红球和
个红球和![]() 个黄球的袋子中摸出的
个黄球的袋子中摸出的![]() 个球恰好是红球;
个球恰好是红球;
![]() 一副去掉大、小王的扑克牌中,随意抽取
一副去掉大、小王的扑克牌中,随意抽取![]() 张,抽到的牌是红桃;
张,抽到的牌是红桃;
![]() 水中捞月;
水中捞月;
![]() 太阳从东方升起;
太阳从东方升起;
![]() 随手翻一下日历,翻到的刚好是周二.
随手翻一下日历,翻到的刚好是周二.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )

A. AD+BC=AB B. 与∠CBO互余的角有两个
C. ∠AOB=90° D. 点O是CD的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.
(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE;
(2)如图2,当点D在线段BC延长线上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.请画出图形。上述结论是否仍然成立,并说明理由;
(3)根据图2,请直接写出AD、BD、CD三条线段之间的数量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BCD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程![]() 的一根为
的一根为![]() .
.
![]() 求
求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 求证:抛物线
求证:抛物线![]() 与
与![]() 轴有两个交点;
轴有两个交点;
![]() 设抛物线
设抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不重合),且以
不重合),且以![]() 为直径的圆正好经过该抛物线的顶点,求
为直径的圆正好经过该抛物线的顶点,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .若有一半径为
.若有一半径为![]() 的圆分别与
的圆分别与![]() 、
、![]() 相切,则下列何种方法可找到此圆的圆心( )
相切,则下列何种方法可找到此圆的圆心( )

A. ![]() 的角平分线与
的角平分线与![]() 的交点
的交点
B. ![]() 的中垂线与
的中垂线与![]() 中垂线的交点
中垂线的交点
C. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点
中垂线的交点
D. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点
中垂线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中.
中.
![]() 利用尺规作图,在BC边上求作一点P,使得点P到AB的距离
利用尺规作图,在BC边上求作一点P,使得点P到AB的距离![]() 的长
的长![]() 等于PC的长;
等于PC的长;
![]() 利用尺规作图,作出
利用尺规作图,作出![]() 中的线段PD.
中的线段PD.
![]() 要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑
要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com