
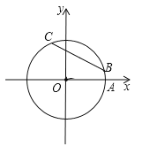
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(5,0),直线y=kx-2k+3(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为____.
【答案】4![]()
【解析】
易知直线y=kx-3k+4过定点D(3,4),运用勾股定理可求出OD,由条件可求出半径OB,由于过圆内定点D的所有弦中,与OD垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题.
对于直线y=kx-3k+4=k(x-3)+4,当x=3时,y=4,
故直线y=kx-3k+4恒经过点(3,4),记为点D.
过点D作DH⊥x轴于点H,
则有OH=3,DH=4,OD=![]() =5.
=5.
∵点A(13,0),
∴OA=13,
∴OB=OA=13.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
BC的最小值为2BD=2![]() =2×
=2×![]() =2×12=24.
=2×12=24.
故答案为:24.


科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图像与x轴和y轴的正半轴分别交于A,B两点.已知OA+OB=6(O为坐标原点),且![]() =4,则这个一次函数的解析式为 ( )
=4,则这个一次函数的解析式为 ( )
A.y=-![]() x+2B.y=-2x+4
x+2B.y=-2x+4
C.y=![]() x+2D.y=-
x+2D.y=-![]() x+2或y=-2x+4
x+2或y=-2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
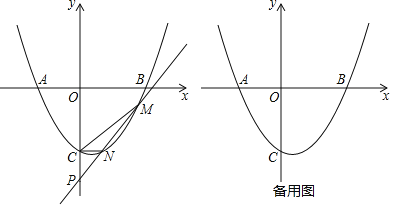
【题目】已知二次函数![]() 的图象对称轴为
的图象对称轴为![]() ,图象交x轴于A,B,交y轴于
,图象交x轴于A,B,交y轴于![]() ,且
,且![]() ,直线
,直线![]() 与二次函数图象交于M,
与二次函数图象交于M,![]() 在N的右边
在N的右边![]() ,交y轴于P.
,交y轴于P.
![]() 求二次函数图象的解析式;
求二次函数图象的解析式;
![]() 若
若![]() ,且
,且![]() 的面积为3,求k的值;
的面积为3,求k的值;
![]() 若
若![]() ,直线AN交y轴于Q,求
,直线AN交y轴于Q,求![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
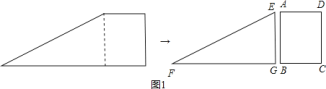
【题目】如图![]() .小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得
.小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得![]() ,
,![]() .在进行如下操作时遇到了下面的几个问题,请你帮助解决.
.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
(1)将![]() 的顶点
的顶点![]() 移到矩形的顶点
移到矩形的顶点![]() 处,再将三角形绕点
处,再将三角形绕点![]() 顺时针旋转使
顺时针旋转使![]() 点落在
点落在![]() 边上,此时,
边上,此时,![]() 恰好经过点
恰好经过点![]() (如图
(如图![]() ),请你求出
),请你求出![]() 和
和![]() 的长度;
的长度;
(2)在(1)的条件下,小明先将三角形的边![]() 和矩形边
和矩形边![]() 重合,然后将
重合,然后将![]() 沿直线
沿直线![]() 向右平移,至
向右平移,至![]() 点与
点与![]() 重合时停止.在平移过程中,设
重合时停止.在平移过程中,设![]() 点平移的距离为
点平移的距离为![]() ,两纸片重叠部分面积为
,两纸片重叠部分面积为![]() ,求在平移的整个过程中,
,求在平移的整个过程中,![]() 与
与![]() 的函数关系式,并求当重叠部分面积为
的函数关系式,并求当重叠部分面积为![]() 时,平移距离
时,平移距离![]() 的值(如图
的值(如图![]() ).
).
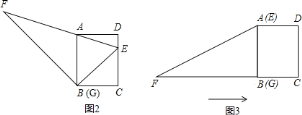
查看答案和解析>>
科目:初中数学 来源: 题型:
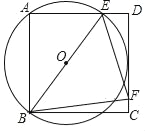
【题目】如图,正方形ABCD的边长为2,点E在边AD上(不与A,D重合),点F在边CD上,且∠EBF=45°,若△ABE的外接圆⊙O与CD边相切.
(1)求⊙O的半径长;
(2)求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是【 】
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
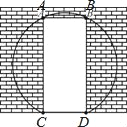
【题目】如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=![]() 米.
米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F
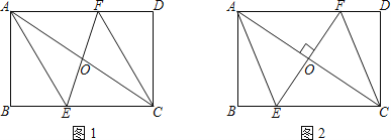
(1)求证:四边形AECF是平行四边形;
(2)如图2,当EF⊥AC时,求EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com