
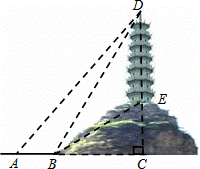
如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米,![]() ≈1.732)
≈1.732)
考点:
解直角三角形的应用-仰角俯角问题.
专题:
应用题.
分析:
设EC=x,则在Rt△BCE中,BC=![]() EC=
EC=![]() x;在Rt△BCD中,CD=
x;在Rt△BCD中,CD=![]() BC=3x;
BC=3x;
在Rt△ACD中,AC=AB+BC=73.2+![]() x,CD=3x,利用关系式AC=CD列方程求出x;
x,CD=3x,利用关系式AC=CD列方程求出x;
塔高DE=CD﹣EC=2x可以求出.
解答:
解:设EC=x(米),
在Rt△BCE中,∠EBC=30°,∴BC=![]() =
=![]() x;
x;
在Rt△BCD中,∠DBC=60°,∴CD=BC•tan60°=![]() x•
x•![]() =3x;
=3x;
在Rt△ACD中,∠DBC=45°,
∴AC=CD,
即:73.2+![]() x=3x,
x=3x,
解得:x=12.2(3+![]() ).
).
塔高DE=CD﹣EC=3x﹣x=2x=2×12.2(3+![]() )=24.4(3+
)=24.4(3+![]() )≈115.5(米).
)≈115.5(米).
答:塔高DE约为115.5米.
点评:
本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度,难度一般.


科目:初中数学 来源: 题型:
 (2013•毕节地区)如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米,
(2013•毕节地区)如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米,| 3 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(贵州毕节卷)数学(解析版) 题型:解答题
如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米,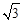 ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米,
如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.(精确到0.1米, ≈1.732)
≈1.732)查看答案和解析>>
科目:初中数学 来源:2013年贵州省毕节地区中考数学试卷(解析版) 题型:解答题
 ≈1.732)
≈1.732)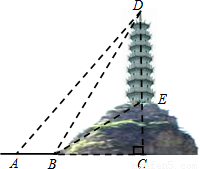
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com