练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若两个正数的算术平均数（即两数和的一半）为2
    		3
    ，几何平均数（即两数积的算术平方根）为
    		3
    ，则这两个数的差是（　　）
    分析：首先设出这两个数，然后根据这两个正数的算术平均数为2
    		3
    ，几何平均数为
    		3
    ，列出等式求出这两个数的和及及积，最后利用完全平方式求解即可．
    解答：解：设这两个数分别为a和b，
    则根据题意得：
    a+b
    2
    =2
    		3
      ①，
    		ab
    =
    		3
      ②，
    ①②两式联立解得：a2+b2=（a+b）2-2ab=48-6=42，
    ∴（a-b）2=a2+b2-2ab=42-2×3=36，
    ∴a-b=±6．
    故选A．
    点评：本题考查算术平方根和完全平方式的知识，解答该类题目的一般思路是分别求出这两个数，但此题行不通，注意整体思想的灵活运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读以下的材料：
    如果两个正数a，b，即a＞0，b＞0，则有下面的不等式：
    a+b
    2
    ≥
    		ab
    当且仅当a=b时取到等号
    我们把
    a+b
    2
    叫做正数a，b的算术平均数，把
    		ab
    叫做正数a，b的几何平均数，于是上述不等式可表述为：两个正数的算术平均数不小于（即大于或等于）它们的几何平均数．它在数学中有广泛的应用，是解决最大（小）值问题的有力工具，下面举一例子：
    例：已知x＞0，求函数y=x+
    4
    x
    的最小值．
    解：另a=x，b=
    4
    x
    ，则有a+b≥2
    		ab
    ，得y=x+
    4
    x
    ≥2
    		x•
    4
    x
    =4    ，当且仅当x=
    4
    x
    时，即x=2时，函数有最小值，最小值为2．
    根据上面回答下列问题
    ①已知x＞0，则当x=
     
    时，函数y=2x+
    3
    x
    取到最小值，最小值为
     
    ；
    ②用篱笆围一个面积为100m2的矩形花园，问这个矩形的长、宽各为多少时，所用的篱笆最短，最短的篱笆是多少？
    ③已知x＞0，则自变量x取何值时，函数y=
    x
    x2-2x+9
    取到最大值，最大值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    若两个正数的算术平均数（即两数和的一半）为数学公式，几何平均数（即两数积的算术平方根）为数学公式，则这两个数的差是


    1. A.
      ±6
    2. B.
      6
    3. C.
      ±36
    4. D.
      36

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    若两个正数的算术平均数（即两数和的一半）为2
    		3
    ，几何平均数（即两数积的算术平方根）为
    		3
    ，则这两个数的差是（　　）
    A．±6B．6C．±36D．36

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年湖北省黄冈市麻城市初三（上）四科联赛数学试卷（解析版） 题型：选择题

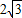    若两个正数的算术平均数（即两数和的一半）为，几何平均数（即两数积的算术平方根）为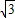，则这两个数的差是（ ）
    A．±6
    B．6
    C．±36
    D．36

    查看答案和解析>>

    同步练习册答案