
ЁОЬтФПЁПЖЫЮчНкЪЧжаЙњЕФДЋЭГНкШеЃЎНёФъЖЫЮчНкЧАЯІЃЌЫьФўЪаФГЪГЦЗГЇГщбљЕїВщСЫКгЖЋФГОгУёЧјЪаУёЖдAЁЂBЁЂCЁЂDЫФжжВЛЭЌПкЮЖєезгбљЦЗЕФЯВАЎЧщПіЃЌВЂНЋЕїВщЧщПіЛцжЦГЩШчЭМСНЗљВЛЭъећЭГМЦЭМЃК
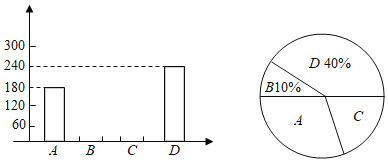
ЃЈ1ЃЉБОДЮВЮМгГщбљЕїВщЕФОгУёгаЁЁ ЁЁШЫЃЎ
ЃЈ2ЃЉЯВЛЖCжжПкЮЖєезгЕФШЫЪ§ЫљеМдВаФНЧЮЊЁЁ ЁЁЖШЃЎИљОнЬтжааХЯЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉШєИУОгУёаЁЧјга6000ШЫЃЌЧыФуЙРМЦАЎГдDжжєезгЕФгаЁЁ ЁЁШЫЃЎ
ЃЈ4ЃЉШєгаЭтаЭЭъШЋЯрЭЌЕФAЁЂBЁЂCЁЂDзизгИївЛИіЃЌжѓЪьКѓЃЌаЁРюГдСЫСНИіЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓЫћЕкЖўИіГдЕФєезгЧЁКУЪЧAжжєезгЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ600ЃЛЃЈ2ЃЉ72ЃЌЭММћНтЮіЃЛЃЈ3ЃЉ2400ШЫЃЛЃЈ4ЛЭММћНтЮіЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгУЯВЛЖDжжПкЮЖєезгЕФШЫЪ§Г§вдЫќЫљеМЕФАйЗжБШЕУЕНЕїВщЕФзмШЫЪ§ЃЛ
ЃЈ2ЃЉЯШМЦЫуГіЯВЛЖBжжПкЮЖєезгЕФШЫЪ§ЃЌдйМЦЫуГіЯВЛЖCжжПкЮЖєезгЕФШЫЪ§ЃЌдђгУ360ЖШГЫвдЯВЛЖCжжПкЮЖєезгЕФШЫЪ§ЫљеМЕФАйЗжБШЕУЕНЫќдкЩШаЮЭГМЦЭМжаЫљеМдВаФНЧЕФЖШЪ§ЃЌШЛКѓВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉгУDеМЕФАйЗжБШГЫвд6000МДПЩЕУЕННсЙћЃЛ
ЃЈ4ЃЉЛЪїзДЭМеЙЪОЫљга12жжЕШПЩФмЕФНсЙћЪ§ЃЌевГіЫћЕкЖўИіГдЕФєезгЧЁКУЪЧAжжєезгЕФНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНтЃЎ
НтЃКЃЈ1ЃЉ240ЁТ40%ЃН600ЃЈШЫЃЉЃЌ
ЫљвдБОДЮВЮМгГщбљЕїВщЕФОгУёга600ШЫЃЛ
ЙЪД№АИЮЊЃК600ЃЛ
ЃЈ2ЃЉЯВЛЖBжжПкЮЖєезгЕФШЫЪ§ЮЊ600ЁС10%ЃН60ЃЈШЫЃЉЃЌ
ЯВЛЖCжжПкЮЖєезгЕФШЫЪ§ЮЊ600Љ180Љ60Љ240ЃН120ЃЈШЫЃЉЃЌ
ЫљвдЯВЛЖCжжПкЮЖєезгЕФШЫЪ§ЫљеМдВаФНЧЕФЖШЪ§ЮЊ360ЁуЁС![]() ЃН72ЁуЃЛ
ЃН72ЁуЃЛ
ВЙШЋЬѕаЮЭГМЦЭМЮЊЃК
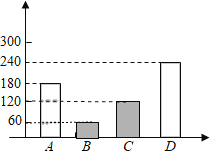
ЙЪД№АИЮЊЃК72ЃЛ
ЃЈ3ЃЉ6000ЁС40%ЃН2400ЃЌ
ЫљвдЙРМЦАЎГдDжжєезгЕФга2400ШЫЃЛ
ЙЪД№АИЮЊ2400ЃЛ
ЃЈ4ЃЉЛЪїзДЭМЮЊЃК
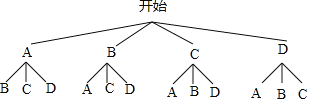
ЙВга12жжЕШПЩФмЕФНсЙћЪ§ЃЌЦфжаЫћЕкЖўИіГдЕФєезгЧЁКУЪЧAжжєезгЕФНсЙћЪ§ЮЊ3ЃЌ
ЫљвдЫћЕкЖўИіГдЕФєезгЧЁКУЪЧAжжєезгЕФИХТЪЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШєЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФЖдГЦжсЮЊx=1ЃЌгыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуAЁЂЕуB(Љ1ЃЌ0)ЃЌдђЂйЖўДЮКЏЪ§ЕФзюДѓжЕЮЊa+b+cЃЛЂкaЉb+cЃМ0ЃЛЂлb2Љ4acЃМ0ЃЛЂмЕБyЃО0ЪБЃЌЉ1ЃМxЃМ3ЃЌЦфжаНсТле§ШЗЕФгаЃЈ ЃЉ
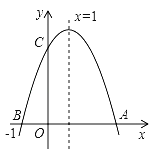
A.ЂйЂлB.ЂйЂмC.ЂйЂкD.ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтБГОАЃЉдкУцЛ§ЖМЯрЕШЕФЫљгаОиаЮжаЃЌЕБЦфжавЛИіОиаЮЕФвЛБпГЄЮЊ![]() ЪБЃЌЫќЕФСэвЛБпГЄЮЊ
ЪБЃЌЫќЕФСэвЛБпГЄЮЊ![]() ЃЎЧѓжмГЄ
ЃЎЧѓжмГЄ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈНЈСЂФЃаЭЃЉ
ЃЈ1ЃЉЩшОиаЮЯрСкСНБпЕФГЄЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌгЩЬтвтПЩЕУ
ЃЌгЩЬтвтПЩЕУ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩжмГЄЮЊ
ЃЌгЩжмГЄЮЊ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌТњзувЊЧѓЕФ
ЃЌТњзувЊЧѓЕФ![]() ЕФШЁжЕЃЌДгЁАЭМаЮЁБНЧЖШПМТЧЃЌгІЪЧКЏЪ§
ЕФШЁжЕЃЌДгЁАЭМаЮЁБНЧЖШПМТЧЃЌгІЪЧКЏЪ§![]() гы ЕФЭМЯѓдкЕквЛЯѓЯоФкгаЙЋЙВЕуЪБ
гы ЕФЭМЯѓдкЕквЛЯѓЯоФкгаЙЋЙВЕуЪБ![]() ЕФШЁжЕЗЖЮЇЃЛДгЁАДњЪ§ЁБНЧЖШПМТЧЃЌгІПДзїЗНГЬ гае§Ъ§НтЪБ
ЕФШЁжЕЗЖЮЇЃЛДгЁАДњЪ§ЁБНЧЖШПМТЧЃЌгІПДзїЗНГЬ гае§Ъ§НтЪБ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈЛЭМЙлВьЃЉ
ЃЈ2ЃЉКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЖјКЏЪ§
ЕФЭМЯѓШчЭМЫљЪОЃЌЖјКЏЪ§![]() ЕФЭМЯѓЪЧвЛЬѕгы
ЕФЭМЯѓЪЧвЛЬѕгы![]() жсЦНааЕФжБЯпЃЎЕБжБЯп
жсЦНааЕФжБЯпЃЎЕБжБЯп![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯѓга
ЕФЭМЯѓга![]() ЮЈвЛЙЋЙВЕуЃЈ ЃЌ ЃЉЪБЃЌжмГЄ
ЮЈвЛЙЋЙВЕуЃЈ ЃЌ ЃЉЪБЃЌжмГЄ![]() ШЁЕУзюаЁжЕЮЊ ЃЎ
ШЁЕУзюаЁжЕЮЊ ЃЎ
ЃЈДњЪ§ЫЕРэЃЉ
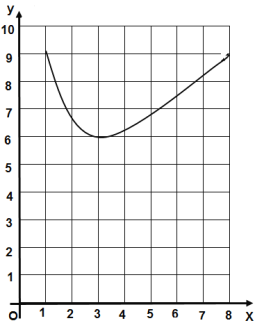
ЃЈ3ЃЉдВдВЫЕОиаЮЕФжмГЄПЩвдЮЊ![]() ЃЌЗНЗНЫЕОиаЮЕФжмГЄПЩвдЮЊ
ЃЌЗНЗНЫЕОиаЮЕФжмГЄПЩвдЮЊ![]() ЃЌФуШЯЮЊдВдВКЭЗНЗНЕФЫЕЗЈЖдТ№ЃПЮЊЪВУДЃП
ЃЌФуШЯЮЊдВдВКЭЗНЗНЕФЫЕЗЈЖдТ№ЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
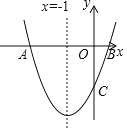
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНx2+bx+cгыxжсНЛгкAЁЂBСНЕуЃЌНЛyжсгкЕуCЃЌABЃН4ЃЌЖдГЦжсЪЧжБЯпxЃНЉ1ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгACЃЌEЪЧЯпЖЮOCЩЯвЛЕуЃЌЕуEЙигкжБЯпxЃНЉ1ЕФЖдГЦЕуFе§КУТфдкACЩЯЃЌЧѓЕуFЕФзјБъЃЛ
ЃЈ3ЃЉЖЏЕуMДгЕуOГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуAдЫЖЏЃЌЕНДяЕуAМДЭЃжЙдЫЖЏЃЌЙ§ЕуMзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуNЃЌНЛЯпЖЮACгкЕуQЃЎЩшдЫЖЏЪБМфЮЊtЃЈtЃО0ЃЉУыЃЎ
ЂйСЌНгBCЃЌШєЁїBOCгыЁїAMNЯрЫЦЃЌЧыжБНгаДГіtЕФжЕЃЛ
ЂкЁїAOQФмЗёЮЊЕШбќШ§НЧаЮЃПШєФмЃЌЧѓГіtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
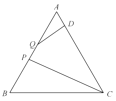
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧБпBCЕФжаЕуЃЌСЌНгAEЁЂDEЃЌЗжБ№НЛBDЁЂACгкЕуPЁЂQЃЌЙ§ЕуPзїPFЁЭAEНЛCBЕФбгГЄЯпгкFЃЌЯТСаНсТлЃК
ЂйЁЯAED+ЁЯEAC+ЁЯEDBЃН90ЁуЃЌ
ЂкAPЃНFPЃЌ
ЂлAEЃН![]() AOЃЌ
AOЃЌ
ЂмШєЫФБпаЮOPEQЕФУцЛ§ЮЊ4ЃЌдђИУе§ЗНаЮABCDЕФУцЛ§ЮЊ36ЃЌ
ЂнCEEFЃНEQDEЃЎ
Цфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ

A.5ИіB.4ИіC.3ИіD.2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧгУКкЩЋЦхзгАкГЩЕФУРРіЭМАИЃЌАДееетбљЕФЙцТЩАкЯТШЅЃЌЕк10ИіетбљЕФЭМАИашвЊКкЩЋЦхзгЕФИіЪ§ЮЊЃЈ ЃЉ

![]()


A.148B.152C.174D.202
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБп![]() ЕФБпГЄЮЊ3ЃЌЕу
ЕФБпГЄЮЊ3ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() дкБп
дкБп![]() ЩЯдЫЖЏЃЌ
ЩЯдЫЖЏЃЌ![]() ЃЌгаЯТСаНсТлЃК
ЃЌгаЯТСаНсТлЃК
Ђй![]() гы
гы![]() ПЩФмЯрЕШЃЛЂк
ПЩФмЯрЕШЃЛЂк![]() гы
гы![]() ПЩФмЯрЫЦЃЛЂлЫФБпаЮ
ПЩФмЯрЫЦЃЛЂлЫФБпаЮ![]() УцЛ§ЕФзюДѓжЕЮЊ
УцЛ§ЕФзюДѓжЕЮЊ![]() ЃЛЂмЫФБпаЮ
ЃЛЂмЫФБпаЮ![]() жмГЄЕФзюаЁжЕЮЊ
жмГЄЕФзюаЁжЕЮЊ![]() ЃЎЦфжаЃЌе§ШЗНсТлЕФађКХЮЊЃЈ ЃЉ
ЃЎЦфжаЃЌе§ШЗНсТлЕФађКХЮЊЃЈ ЃЉ
A.ЂйЂмB.ЂкЂмC.ЂйЂлD.ЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌАыОЖЮЊ2ЕФ
жаЃЌАыОЖЮЊ2ЕФ![]() гы
гы![]() жсЕФе§АыжсНЛгкЕу
жсЕФе§АыжсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЩЯвЛЖЏЕуЃЌЕу
ЩЯвЛЖЏЕуЃЌЕу![]() ЮЊЯв
ЮЊЯв![]() ЕФжаЕуЃЌжБЯп
ЕФжаЕуЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() УцЛ§ЕФзюаЁжЕЮЊ________ЃЎ
УцЛ§ЕФзюаЁжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
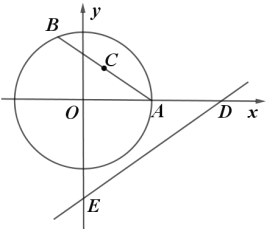
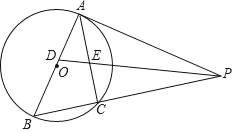
ЁОЬтФПЁПШчЭМЃЌвдABЮЊжБОЖЕФЁбOЭтНггкЁїABCЃЌЙ§AЕуЕФЧаЯпAPгыBCЕФбгГЄЯпНЛгкЕуPЃЌЁЯAPBЕФЦНЗжЯпЗжБ№НЛABЃЌACгкЕуDЃЌEЃЌЦфжаAEЃЌBDЃЈAEЃМBDЃЉЕФГЄЪЧвЛдЊЖўДЮЗНГЬx2Љ5x+6=0ЕФСНИіЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓжЄЃКPABD=PBAEЃЛ
ЃЈ2ЃЉдкЯпЖЮBCЩЯЪЧЗёДцдквЛЕуMЃЌЪЙЕУЫФБпаЮADMEЪЧСтаЮЃПШєДцдкЃЌЧыИјгшжЄУїЃЌВЂЧѓЦфУцЛ§ЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com