
分析 (1)首先化简二次根式进而合并求出答案;
(2)直接利用乘法公式计算得出答案;
(3)直接利用二次根式乘法运算法则求出答案;
(4)直接利用二次根式除法运算法则计算进而得出答案.
解答 解:(1)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(2)($\sqrt{5}$-3)2+($\sqrt{11}$-3)($\sqrt{11}$+3)
=5+9-6$\sqrt{5}$+11-9
=16-6$\sqrt{5}$;
(3)($\sqrt{8}$+$\sqrt{3}$)×$\sqrt{6}$
=$\sqrt{8×6}$+$\sqrt{3×6}$
=4$\sqrt{3}$+3$\sqrt{2}$;
(4)(4$\sqrt{2}$-3$\sqrt{6}$)÷2$\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$
=4$\sqrt{2}$÷2$\sqrt{2}$-3$\sqrt{6}$÷2$\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$
=2-$\frac{3\sqrt{3}}{2}$+$\frac{3\sqrt{3}}{2}$
=2.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.
如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的顶点A(-1,0),B(3,0),D(-1,2),CD交y轴于E;抛物线y=ax2+bx+c经过点A,B,且该抛物线的顶点为M.
如图,矩形ABCD的顶点A(-1,0),B(3,0),D(-1,2),CD交y轴于E;抛物线y=ax2+bx+c经过点A,B,且该抛物线的顶点为M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
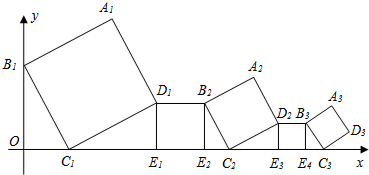
| A. | ($\frac{1}{2}$)2014 | B. | ($\frac{1}{2}$)2015 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
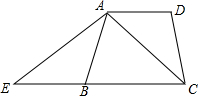 如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE,AC,∠ADC+∠ABC=180°.
如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE,AC,∠ADC+∠ABC=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com