
����Ŀ����֪��ABC�ǵȱ������Σ��ı���ADEF�����Σ���ADE=120����AD��AB����
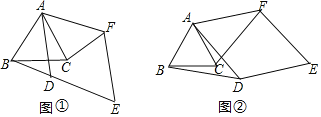
��1����ͼ�٣���AD���BC�ཻ����D���F��ֱ��AC������ʱ��BD��CF��������ϵΪ___________��
��2����ͼ���е�����ADEF�Ƶ�A��ƽ������ʱ����ת����0��������180������
���жϣ�1���еĽ����Ƿ���Ȼ������������ͼ��֤����Ľ��ۣ�
����AC=4��AD=6������ACEΪֱ��������ʱ��ֱ��д��CE�ij��ȣ�
���𰸡���1��![]() ����2��I��1���еĽ�����Ȼ�������������������II
����2��I��1���еĽ�����Ȼ�������������������II![]() ��
��![]()
��������
��1�����ݵ�ʽ�����ʵó���BAD=��CAF������SAS֤����ABD����ACFȫ�ȣ�������ȫ�������ε����ʵó����ɣ�
��2��I�����ݵ�ʽ�����ʵó���BAD=��CAF������SAS֤����ABD����ACFȫ�ȣ�������ȫ�������ε����ʵó����ɣ�
II������ACE��ֱ��������ʱ���������������
����ͼ2������ACE=90��ʱ������ͼ3������EAC=90��ʱ�����ɶ������ɵ�CE�ij���
��1���⣺��ͼ�٣����ı���ADEF�����Σ���ADE=120����
��AD=AF����DAF=60����
���DAC+��CAF=60����
�ߡ�ABC�ǵȱ������Σ�
��AB=AC����BAC=60����
���BAD+��DAC=60����
���BAD=��CAF��
���BAD�ա�CAF��SAS����
��BD=CF��
�ʴ�Ϊ��BD=CF��
��2��I����1���еĽ�����Ȼ������
֤������ͼ�ڣ��ߡ�ABC�ǵȱ������Σ�
��AB=AC����BAC=60����
������ADEF��
��AD=AF��AF��DE��
���DAF=180��-��ADE=180��-120��=60����
���BAC=��DAF��
����BAC+��CAD=��DAF+��CAD��
���BAD=��CAF��
���BAD�ա�CAF��
��BD=CF��
II������ACE��ֱ��������ʱ���������������
����ͼ2������ACE=90��ʱ����F��FG��AE��G��

���ı���ADEF�����Σ�
��AF=FE����AFE=��ADE=120����
���AFG=60����
���FAG=30����
��AF=AD=6��
��FG=3��
��AG=3![]() ��
��
��AE=2AG=6![]() ��
��
Rt��ACE��CE=![]() =
=![]() ��
��
����ͼ3������EAC=90��ʱ��ͬ���ã�AE=6![]() ��
��
�ɹ��ɶ����ã�CE=![]() =
=![]() ��
��

����������CE�ij�Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
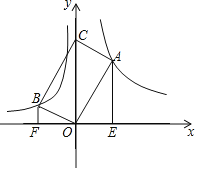
����Ŀ����ͼ����A��B��x����Ϸ�����AOB��90����OA��OB�ֱ��뺯��![]() ��
��![]() ��ͼ����A��B���㣬��OA��OBΪ�ڱ�������AOBC������C��y����ʱ���ֱ����A�͵�B��AE��x�ᣬBF��x�ᣬ����ֱ�ΪE��F����
��ͼ����A��B���㣬��OA��OBΪ�ڱ�������AOBC������C��y����ʱ���ֱ����A�͵�B��AE��x�ᣬBF��x�ᣬ����ֱ�ΪE��F����![]() ��_______��
��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����һ���ֻ�֧�ܣ�����֧�ܵĴ�ϸ���õ����ļṹͼ��ͼ��2����ʾ����֪֧�ܵײ�֧��CDƽ����ˮƽ�棬EF��OE��GF��EF��֧�ܿ��Ƶ�O��ת��OE��20cm��EF��20![]() cm����ͼ��3������֧���ϲ���O����ʱ����ת������G����ֱ��CD��ʱ�������á�EOG��65�㣮
cm����ͼ��3������֧���ϲ���O����ʱ����ת������G����ֱ��CD��ʱ�������á�EOG��65�㣮
��1����FG�ij��ȣ������ȷ��0.1����
��2����֧����ͼ��3��ת��ͼ��4����λ�ã�����ʱF��O�������ڵ�ֱ��ǡ����CD��ֱ����F���˶�·�ߵij��ȳ�Ϊ��F��·���������F��·������
���ο����ݣ�sin65���0.91��cos65���0.42��tan65���2.14��1.73��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
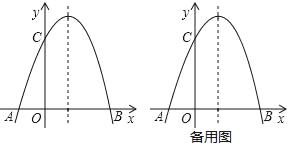
����Ŀ����֪��������y����x2+bx+c������A����1��0����C��0��3������1���������ߵĽ���ʽ����2���������ߵĶԳ����ϣ��Ƿ���ڵ�P��ʹPA+PC��ֵ��С��������ڣ��������P�����꣬��������ڣ���˵�����ɣ���3�����M�������ߵĶԳ����ϣ�����MAC��ֱ��������ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ˡ��������꼶����ѧ��180�ˣ�Ϊ�˽��������꼶ѧ�������ʽ�������������˳������飬����������£�
�����ռ�����
�Ӱˡ��������꼶�������ȡ20��ѧ���������ʽ������ԣ����Գɼ����ٷ��ƣ����£�
���꼶 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
���꼶 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
��������������
���ɼ������·ֶ������������������������ݣ�
�ɼ���x�� | 40��x��49 | 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
���꼶���� | 0 | 0 | 1 | 11 | 7 | 1 |
���꼶���� | 1 | 0 | 0 | 7 | 10 | 2 |
��˵�����ɼ�80�ּ�����Ϊ���ʽ������㣬70��79��Ϊ���ʽ������ã�60��69��Ϊ���ʽ����ϸ�60������Ϊ���ʽ������ϸ�
������������
�����������ݵ�ƽ��������λ�������������������ʾ��
�꼶 | ƽ���� | ��λ�� | ���� | ���� |
���꼶 | 78.3 | 77.5 | 75 | 33.6 |
���꼶 | 78 | 80.5 | a | 52.1 |
��1��������a��ֵΪ______��
��2��������Ƹ�У���꼶���ʽ��������ѧ������Ϊ���٣�
��3������������Ϣ������Ϊ�ĸ��꼶ѧ�������ʽ����������һЩ����˵�����ɣ������������ͬ�ĽǶ�˵���ƶϵĺ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������� y��![]() ��ͼ����ͼ��ʾ������κ��� y =ax 2��2x��һ�κ��� y��bx+a ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
��ͼ����ͼ��ʾ������κ��� y =ax 2��2x��һ�κ��� y��bx+a ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��

A. B.
B. C.
C.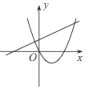 D.
D.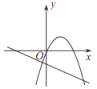
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���ξ���Ϊ�����οͣ�����һ�����������ľջ�� AB ��ջ�� AB �뾰����·CD ƽ�У��� C �����ջ��һ�� A λ�ڱ�ƫ�� 42�㷽���� D �����ջ����һ�� B λ�ڱ�ƫ�� 32�㷽����֪ CD ��120 m �� BD ��80 m ����ľջ�� AB �ij��ȣ�������������� ��
(�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() )
)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ������O�ֱ�BC�ڵ�D����CA���ӳ����ڵ�E������D��DH��AC������Ϊ��H������DE����AB�ڵ�F��
��1����֤��DH����O�����ߣ�
��2������O�İ뾶Ϊ4��
����AE��FEʱ����![]() �ij����������������
�ij����������������
����![]() ʱ�����߶�AF�ij���
ʱ�����߶�AF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��1��y����x+1��x�ᡢy��ֱ��ڵ�B����E��������L��y��ax2+bx+c������B����A����3��0���͵�C��0����3��������ֱ��l������һ��D��

��1����������L�Ľ���ʽ��
��2����PΪx����һ����
����ͼ2������P��x��Ĵ��ߣ���ֱ��1���ڵ�M����������L���ڵ�N������P�ڵ�A����B֮���˶�ʱ�����ı���AMBN��������ֵ��
������AD��AC��CP������PCA����ADBʱ�����P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com