
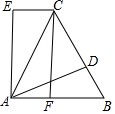
 如图,△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置.科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
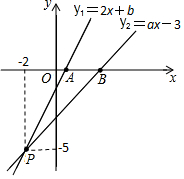 如图,已知函数y1=2x+b和y2=ax-3的图象交于点P (-2,-5),这两个函数的图象与x轴分别交于点A、B.
如图,已知函数y1=2x+b和y2=ax-3的图象交于点P (-2,-5),这两个函数的图象与x轴分别交于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
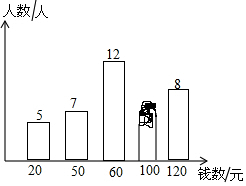 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com