
 如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.
如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.| AE |
| AF |
| AC |
| AB |

| AE |
| AD |
| AD |
| AB |
| AE |
| AF |
| AC |
| AB |


科目:初中数学 来源: 题型:
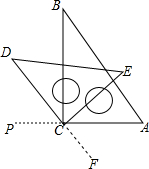 小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C重合,摆放成如图所示,延长DC至点F,∠PCD与∠ACF就是一组对顶角.
小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C重合,摆放成如图所示,延长DC至点F,∠PCD与∠ACF就是一组对顶角.查看答案和解析>>
科目:初中数学 来源: 题型:
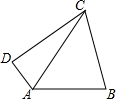 如图,四边形ABCD中,∠BAD=120°,∠BCD=60°,对角线AC平分∠BAD.
如图,四边形ABCD中,∠BAD=120°,∠BCD=60°,对角线AC平分∠BAD.查看答案和解析>>
科目:初中数学 来源: 题型:
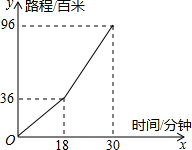 “懒洋洋”由于身体太胖,决定每天早上起来锻炼身体,帮助减肥,已知“懒洋洋”从“羊村”出发到森林里,先上坡后下坡,行程状况如图所示;若返回时上坡和下坡的速度扔保持不变,那么“懒洋洋”从森林到“羊村”所用的时间是
“懒洋洋”由于身体太胖,决定每天早上起来锻炼身体,帮助减肥,已知“懒洋洋”从“羊村”出发到森林里,先上坡后下坡,行程状况如图所示;若返回时上坡和下坡的速度扔保持不变,那么“懒洋洋”从森林到“羊村”所用的时间是查看答案和解析>>
科目:初中数学 来源: 题型:
 已知∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB,根据图填空.
已知∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB,根据图填空.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com