
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,
内部,![]() 时,
时,![]() ________.
________.
(2)当圆心![]() 在
在![]() 内部,四边形
内部,四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的度数;
的度数;
(3)当圆心![]() 在
在![]() 外部,四边形
外部,四边形![]() 为平行四边形时,请直接写出
为平行四边形时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
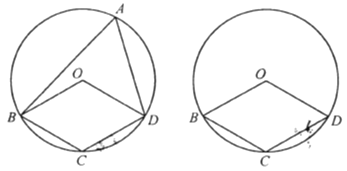
【答案】120
【解析】试题分析:(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠OAB+∠OAD=∠ABO+∠ADO=60°,然后根据圆周角定理易得∠BOD=2∠BAD=120°;
(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠A,则∠BCD=2∠A,然后根据圆内接四边形的性质由∠BCD+∠A=180°,易计算出∠A的度数;
(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD-∠OAB=∠ADO-∠ABO=∠BAD,由(2)得∠BAD=60°,
所以∠ADO-∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO-∠ADO=60°.
解: (1)连接OA,如图1,
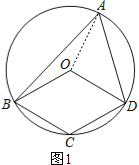
∵OA=OB,OA=OD,
∵∠OAB=∠ABO,∠OAD=∠ADO,
∴∠OAB+∠OAD=∠ABO+∠ADO=60°,即∠BAD=60°,
∴∠BOD=2∠BAD=120°;
故答案为120°;
(2)∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,
∵∠BOD=2∠A,
∴∠BCD=2∠A,
∵∠BCD+∠A=180°,即3∠A=180°,
∴∠A=60°;
(3)当∠OAB比∠ODA小时,如图2,
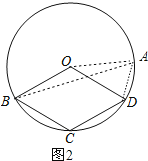
∵OA=OB,OA=OD,
∵∠OAB=∠ABO,∠OAD=∠ADO,
∴∠OAD∠OAB=∠ADO∠ABO=∠BAD,
由(2)得∠BAD=60°,
∴∠ADO∠ABO=60°;
当∠OAB比∠ODA大时,
同理可得∠ABO∠ADO=60°,
综上所述,![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
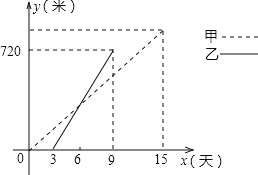
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
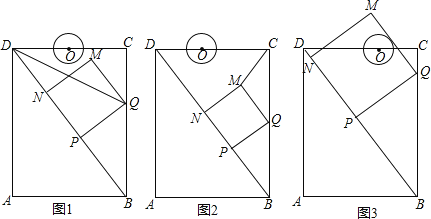
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四项调查中,方式正确的是![]()
![]()
A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,已知该小区用水量不超过![]() 的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
级别 |
|
|
|
|
|
|
月均用水量 |
|
|
|
|
|
|
频数(户) | 6 | 12 |
| 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)补全频率分布直方图;
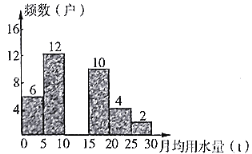
(3)若将调查数据绘制成扇形统计图,则月均用水量“![]() ”的圆心角度数是 .
”的圆心角度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中放有3个红球和5个白球,乙口袋中放有7个红球和9个白球,所有球除颜色外都相同.充分搅匀两个口袋,分别从两个口袋中任意摸出一个球,设从甲中摸出红球的概率是![]() (红),从乙中摸出红球的概率是
(红),从乙中摸出红球的概率是![]() (红).
(红).
(1)求![]() (红)与
(红)与![]() (红)的值,并比较它们的大小.
(红)的值,并比较它们的大小.
(2)将甲、乙两个口袋的球都倒入丙口袋,充分搅匀后,设从丙中任意摸出一球是红球的概率为![]() (红).小明认为:
(红).小明认为:![]() (红)
(红)![]()
![]() (红)
(红)![]()
![]() (红).他的想法正确吗?请说明理由.
(红).他的想法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com