
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,点P是CB边上的一点,且tan∠PAC=![]() ,⊙O是△APB的外接圆.
,⊙O是△APB的外接圆.
(1)求证:∠PAC=∠ABC;
(2)求证:AC是⊙O的切线;
(3)求⊙O的半径.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)通过证明△ACP∽△BCA,可得∠PAC=∠ABC;
(2)作直径AD,交⊙O于点D,连结PD,由圆周角定理可求∠PDA=∠PAC=∠ABC,可证AD⊥AC,即可得⊙O与直线AC的位置关系;
(3)利用锐角三角函数可求CP,PD的长,由勾股定理可求AP的长,AD的长,可得⊙O的半径.
解:(1)证明:在Rt△ACP中,tan∠PAC=![]() =
=![]() ,
,
∵AC=2,BC=4,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠PCA=∠ACB=90°,
∴△ACP∽△BCA,
∴∠PAC=∠ABC;
(2)证明:如图,作⊙O的直径AD,交⊙O于点D,连接PD,
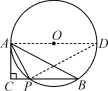
∵AD为⊙O的直径,
∴∠APD=90°,
∴∠PAD+∠PDA=90°,
∵∠PDA=∠ABC,∠PAC=∠ABC,
∴∠PDA=∠PAC,
∴∠PAC+∠PAD=90°,
∴∠CAD=90°,
∴AD⊥AC,
∵AD为⊙O的直径,
∴AC是⊙O的切线;
(3)∵tan∠PAC=![]() =
=![]() ,AC=2,
,AC=2,
∴PC=1,
∴AP=![]() =
=![]()
∵∠PDA=∠PAC,
∴tan∠PAC=tan∠PDA=![]() =
=![]() ,
,
∴PD=2AP=![]() ,
,
∴AD=![]() ,
,
∴⊙O的半径为![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
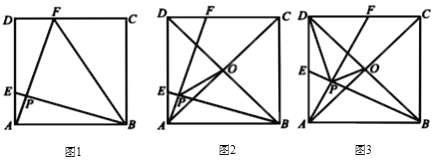
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)如图1,连接![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如图3,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,
,![]() ,若
,若![]() ,试探索
,试探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.4cm,CD=8cm,AB=40cm,BC=45cm,
 图1
图1
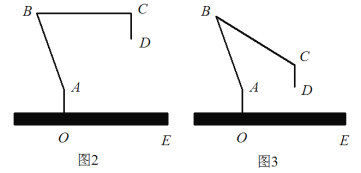
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °
②投影探头的端点D到桌面OE的距离
(2)如图3,将(1)中的BC向下旋转,∠ABC=30°时,求投影探头的端点D到桌面OE的距离
(参考数据:sin70≈0.94,cos70≈0.34,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
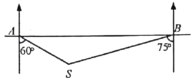
【题目】一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 在船的南偏东60°方向,轮船继续向正东航行30海里后到达
在船的南偏东60°方向,轮船继续向正东航行30海里后到达![]() 处,这时测得灯塔
处,这时测得灯塔![]() 在船的南偏西75°方向,则灯塔
在船的南偏西75°方向,则灯塔![]() 离观测点
离观测点![]() 、
、![]() 的距离分别是( )
的距离分别是( )
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC与△DEF均为等边三角形,且AB=2,DB=1,现△ABC静止不动,△DEF沿着直线EC以每秒1个单位的速度向右移动设△DEF移动的时间为x,△DEF与△ABC重合的面积为y,则能大致反映y与x函数关系的图象是( )
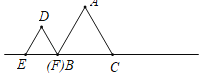
A.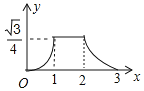 B.
B.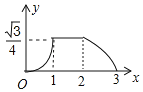
C. D.
D.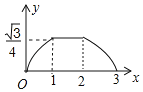
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
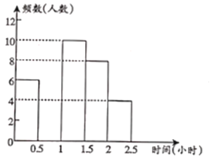
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() ,
,![]() ,
,![]() 为格点,
为格点,![]() 为小正方形边的中点.
为小正方形边的中点.
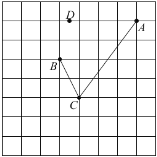
(1)![]() 的长等于_________;
的长等于_________;
(2)点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段
取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段![]() ,
,![]() ,并简要说明点
,并简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
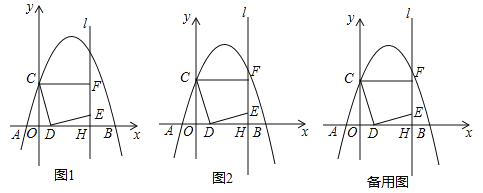
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
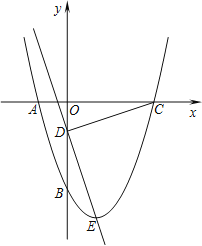
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com