
【题目】某书店店主对书店销售情况进行统计,店主根据一个月内平均每天各销售时间段内的销售量,绘制了如下尚不完整的统计图表.
销售情况扇形统计图
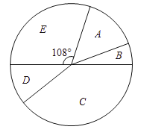
销售情况统计表
销售时间段 | 销售数量(本) |
| 16 |
|
|
| 37 |
| 12 |
| 30 |
合计 |
|
根据以上信息,回答下列问题:
(1)平均每天的销售总量![]() ________,
________,![]() 时间段每天的销售数量
时间段每天的销售数量![]() ___________.
___________.
(2)求出![]() 时间段所在扇形的圆心角的度数.
时间段所在扇形的圆心角的度数.
(3)若该书店一年的销量有32000本,请你估计![]() 时间段全年卖出多少本.
时间段全年卖出多少本.
(4)若书店决定减少成本,同时保证销量,决定在某时间段闭店,请你提出一条合理化的建议.
【答案】(1)100,5;(2)18°;(3)估计![]() 时间段全年卖出5120本;(4)老板应在
时间段全年卖出5120本;(4)老板应在![]() 时间段闭店较为合理.
时间段闭店较为合理.
【解析】
(1)根据E的圆心角和销售数量,列出算式计算即可;
(2)用360°乘以B时间段所占的百分比,即可求出所在扇形的圆心角的度数;
(3)用全年销量乘以A时间段所占的百分比,即可求出A时间段全年卖出多少本;
(4)根据统计表,选择在销量最少的时间段闭店即可.
解:(1)由扇形统计图,可知![]() 时间段的销售量所占的百分比为
时间段的销售量所占的百分比为![]() ,
,
∴销售总量为![]() (本),即
(本),即![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() 时间段所在扇形的圆心角的度数为18;
时间段所在扇形的圆心角的度数为18;
(3)![]() (本),
(本),
则估计![]() 时间段全年卖出5120本;
时间段全年卖出5120本;
(4)为了保证销售量,应该选择在销量最少的时间段闭店,故老板应在![]() 时间段闭店较为合理.
时间段闭店较为合理.


科目:初中数学 来源: 题型:
【题目】某水果商在今年1月份用2.2万元购进![]() 种水果和
种水果和![]() 种水果共400箱.其中
种水果共400箱.其中![]() 、
、![]() 两种水果的数量比为5:3.已知
两种水果的数量比为5:3.已知![]() 种水果的售价是
种水果的售价是![]() 种水果售价的2倍少10元,预计当月即可全部售完.
种水果售价的2倍少10元,预计当月即可全部售完.
(1)该水果商想通过本次销售至少盈利8000元,则每箱![]() 水果至少卖多少元?
水果至少卖多少元?
(2)若![]() 、
、![]() 两种水果在(1)的价格销售,但在实际销售中,受市场影响,
两种水果在(1)的价格销售,但在实际销售中,受市场影响,![]() 水果的销量还是下降了
水果的销量还是下降了![]() ,售价下降了
,售价下降了![]() ;
;![]() 水果的销量下降了
水果的销量下降了![]() ,但售价不变.结果
,但售价不变.结果![]() 、
、![]() 两种水果的销售总额相等.求
两种水果的销售总额相等.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
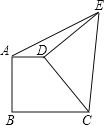
A. 1 B. 2 C. 3 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(1,0),已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.
(1)当抛物线经过点A时.
①求顶点P的坐标;
②设直线l:y=3x+1与抛物线交于B、C两点,抛物线上的点M的横坐标为n(﹣1≤n≤3),过点M作x轴的垂线,与直线l交于点Q,若MQ=d,当d随n的增大而减少时,求n的取值范围.
(2)无论m取何值,该抛物线都经过定点H,当∠AHP=45°时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD中,AB=5,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F.
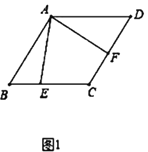
(1)如图1所示,当点E、F分别在边BC、CD上时,求CE+CF的值;
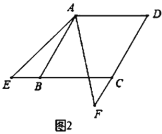
(2)如图2所示,当点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 的延长线时,请从
的延长线时,请从![]() ,
,![]() 两题中任选一题作答,我选______题.
两题中任选一题作答,我选______题.
![]() 题:则
题:则![]() 的值是________.
的值是________.
![]() 题:则
题:则![]() 与
与![]() 的关系是________.
的关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与直线
,与直线![]() 交于点
交于点![]() 和点
和点![]() ,
,![]() 为抛物线的顶点,直线
为抛物线的顶点,直线![]() 是抛物线的对称轴.
是抛物线的对称轴.
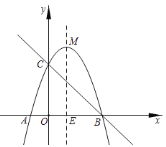
(1)求抛物线的解析式及点![]() 的坐标.
的坐标.
(2)点![]() 为直线
为直线![]() 上方抛物线上一点,设
上方抛物线上一点,设![]() 为点
为点![]() 到直线
到直线![]() 的距离,当
的距离,当![]() 有最大值时,求点
有最大值时,求点![]() 的坐标.
的坐标.
(3)若点![]() 为直线
为直线![]() 上一点,作点
上一点,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是直角三角形时,直接写出点
是直角三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=135°;④BC+FG=
;③∠AFG=135°;④BC+FG=![]() .其中正确的结论是_____.(填入正确的序号)
.其中正确的结论是_____.(填入正确的序号)
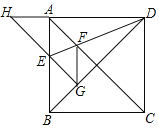
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣4,2),C(﹣6,4),先将△ABC沿一确定方向平移得到△A1B1C1,点C的对应点为点C1的坐标是(﹣4,﹣2),再将△A1B1C1将绕点O逆时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求在这两次变过程中,点B经过点B1到达点B2的路径总长(结果保留π);
(4)△A2B2C2可看成将△ABC以某点为旋转中心,逆时针旋转90°而得,则旋转中心的坐标是 .
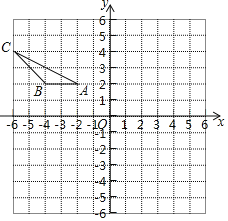
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com