
【题目】已知某的士的起步价为10元(可以坐3千米的路程),若超过3千米,则超出部分每千米另外加收2 元.
(1)小明坐该的士走了x千米的路程,应该付费多少元?
(2)小芳坐该的士走了18千米的路程,应该付费多少元?
【答案】(1) 小明坐该的士走了x(![]() )千米的路程,应该付费10元;小明坐该的士走了x(x>3)千米的路程,应该付费(2x+4)元;(2) 小芳坐该的士走了18千米的路程,应该付费40元
)千米的路程,应该付费10元;小明坐该的士走了x(x>3)千米的路程,应该付费(2x+4)元;(2) 小芳坐该的士走了18千米的路程,应该付费40元
【解析】
(1)分两种情况分析,当![]() 当x>3时,可根据行程超过3千米时,每千米收2元,根据等量关系:起步价+超过3千米的钱数求解即可;
当x>3时,可根据行程超过3千米时,每千米收2元,根据等量关系:起步价+超过3千米的钱数求解即可;
(2) 代入有关数值求解即可.
(1)当![]() 时,应付费10元;
时,应付费10元;
当x>3时,应付费: ![]() =10+2x-6=2x+4,
=10+2x-6=2x+4,
答:小明坐该的士走了x(![]() )千米的路程,应该付费10元;小明坐该的士走了x(x>3)千米的路程,应该付费(2x+4)元.
)千米的路程,应该付费10元;小明坐该的士走了x(x>3)千米的路程,应该付费(2x+4)元.
(2) 当x=18时, 2x+4=2×18+4=40(元),
答:小芳坐该的士走了18千米的路程,应该付费40元.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:
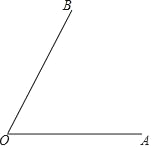
【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴的负半轴交于点A,B(点A在点B的右边),与y轴的正半轴交于点C,且OA=OC=1,则下列关系中正确的是( ) 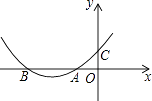
A.a+b=1
B.b<2a
C.a﹣b=﹣1
D.ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,﹣3),且顶点坐标为(﹣1,﹣4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
(1)若AB=10cm,则MN= cm;
(2)若AC=3cm,CP=1cm,求线段PN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.
请回答问题:
![]()
(1)A、B两点间的距离是_____,若点M到点A、点B的距离相等,那么x的值是_____;
(2)若点A先沿着数轴向右移动6个单位长度,再向左移动4个单位长度后所对应的数字是 ____ ;
(3)当x为何值时,点M到点A、点B的距离之和是8;
(4)如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品公司为指导某种应季商品的生产和销售,在对历年市场行情和生产情况进行调查基础上,对今年这种商品的市场售价和生产成本进行了预测并提供了两个方面的信息:如图(1)(2). 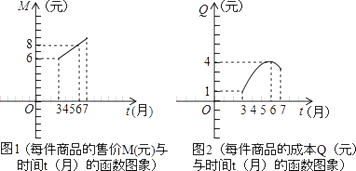
注:两图中的每个实心黑点所对应的纵坐标分别指相应月份一件商品的售价和成本,生产成本6月份最高;图(1)的图象是线段,图(2)的图象是抛物线.
(1)在3月份出售这种商品,一件商品的利润是多少?
(2)设t月份出售这种商品,一件商品的成本Q(元),求Q关于t的函数解析式.
(3)设t月份出售这种商品,一件商品的利润W(元),求W关于t的函数解析式.
(4)问哪个月出售这种商品,一件商品的利润最大?简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB
(1)请用尺规按下列要求作图:
①延长线段AB到C,使BC=AB,
②延长线段BA到D,使AD=AC(不写画法,当要保留画图痕迹)
(2)请直接回答线段BD与线段AC长度之间的大小关系
(3)如果AB=2cm,请求出线段BD和CD的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小华遇到这样一个问题:
已知:如图1,在△ABC中,三边的长分别为AB= ![]() ,AC=
,AC= ![]() ,BC=2,求∠A的正切值.
,BC=2,求∠A的正切值.
小华是这样解决问题的:
如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.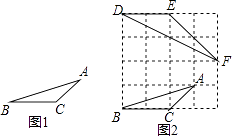
(1)如图2,△DEF中与∠A相等的角为 , ∠A的正切值为 .
(2)参考小华的方法请解决问题:若△LMN的三边分别为LM=2,MN=2 ![]() ,LN=2
,LN=2 ![]() ,求∠N的正切值.
,求∠N的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com