
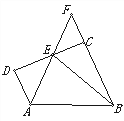
【题目】如图,梯形ABCD中,AD∥BC,∠D=90°,BC=CD=12,∠ABE=45°,点E在DC上,AE,BC的延长线相交于点F,若AE=10,则S△ADE+S△CEF的值是______ .
【答案】30或48
【解析】
如图,首先把梯形补成正方形,然后把△BEC旋转到△BMN的位置,根据它们条件容易证明:△ANB和△ABE全等,故AE=AN=10,设CE=x,然后用x表示AM,AD,DE在根据△ADE是直角三角形利用勾股定理建立关于x的方程,解方程求出x,就可以求出S△ADE+S△CEF的值.
如图,延长DA,过B作BM⊥DA,交其延长线于M.
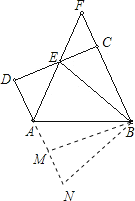
∴四边形DCBM是正方形,
∴DM=BC=CD=12,再把△BEC旋转到△BMN的位置,
∴BN=BE,∠EBC=∠MBN,CE=MN
∵∠ABE=45°
∴∠EBC+∠ABM=90°-45°=45°
∴∠ABN=∠ABM+∠MBN=45°,AB公共
∴△ABN≌△ABE
∴AN=AE=10,设CE=x,那么MN=x,DE=CD-CE=12-x,AM=10-x,AD=12-AM=2+x,
在Rt△ADE中:AD2+DE2=AE2
∴(2+x)2+(12-x)2=102
∴x1=4,x2=6,
当x=4时,CE=4,DE=8,AD=6
∵AD∥CF
∴△ADE∽△FCE,
∴![]() ,
,
∴CF=3,
∴S△ADE+S△CEF=30;
当x=6时,CE=6,DE=6,AD=8
∵AD∥CF
∴△ADE∽△FCE
∴![]() ,
,
∴CF=8
∴S△ADE+S△CEF=48.
综上所述,S△ADE+S△CEF的值是30或48.
故答案为:30或48.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在点P使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动的时间t的值,若不存在,请说明理由.
(4)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
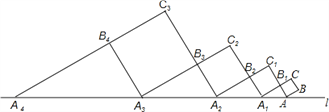
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
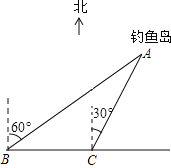
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
查看答案和解析>>
科目:初中数学 来源: 题型:
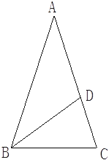
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,
(1)求证:△ABC∽△BCD;
(2)若BC=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
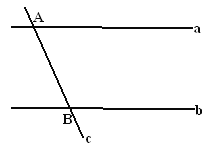
【题目】如图,a、b、c是三条公路,且a∥b,加油站M到三条公路的距离相等.(1)确定加油站M的位置.(保留作图痕迹,不写作法)
(2)一辆汽车沿公路c由A驶向B,行使到AB中点时,司机发现油料不足,仅剩15升汽油,需要到加油站加油,已知从AB中点有路可直通加油站,若AB相距200千米,汽车每行使100千米耗油12升,请判断这辆汽车能否顺利到达加油站?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
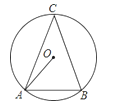
【题目】如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
(3)若点C平分优弧AB,且BC2=3OA2 ,试求α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
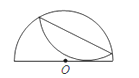
【题目】一张半径为2的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O为半圆圆心,如果切点分直径之比为3:1,则折痕长为( )
A. 3 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com