
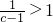 ,
, ,
, ,
,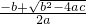 ,x2=
,x2=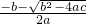 ,
, =
=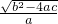 =
=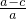 =1-
=1- >1.
>1. ,又b=2,代入其中得到x=-
,又b=2,代入其中得到x=-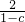 ,而二次函数图象与y轴的交点在直线y=1与y=2之间,由此得到1<c<2,利用这个结论即可解决问题;
,而二次函数图象与y轴的交点在直线y=1与y=2之间,由此得到1<c<2,利用这个结论即可解决问题;

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:选择题
已知二次函数y=ax²+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax²+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax²+bx+c(c≠0)的图像如图4所示,下列说法错误的是:
(A)图像关于直线x=1对称
(B)函数y=ax²+bx+c(c ≠0)的最小值是 -4
(C)-1和3是方程ax²+bx+c=0(c ≠0)的两个根
(D)当x<1时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com