
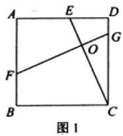
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).

【答案】![]()
【解析】(1)过点B作BM∥FG交CD于M ,构造三角形,证△BCM≌△CDE,可得; CE=BM=FG;(2) 过点B作BM∥FG交CD于M , 连接MO,由(1)证BC=BO,再证MC=MO=MG=ED,又AD=3DE,所以![]() ;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
又BM=CE=![]() ,再根据面积公式得OC=2×
,再根据面积公式得OC=2×![]() .
.
(1)过点B作BM∥FG交CD于M ,

易证四边形FBMG为平行四边形
∴FG=BM,
由BC=CD;∠BCM=∠CDE;∠MBC=∠ECD
可证△BCM≌△CDE,
∴CE=BM=FG;
(2)过点B作BM∥FG交CD于M ,

由(1)知△BCM≌△CDE,又∠OBC=2∠DCE ,
MC=ED,∠MBC=∠DCE=∠MBO,
由BM∥FG得MB⊥CE,
∴∠BOC=∠BCO,
∴BC=BO,连接MO,
∴BM垂直平分OC,
∴MC=MO,
又∵∠GOM=∠BMO=∠BMC=∠OGM
∴MC=MO=MG=ED,
又AD=3DE,
∴![]() ;
;
(3)∵AD=3,
∴由(1)(2)可得
DE=OM=1,BO=AD=3,∴BM=CE=![]() ,
,
OC=2×![]() =2×
=2×![]() =
= ![]() ,
, ![]()
![]()
∴OE=CE-CO=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将一段12cm长的管道竖直置于地面,并在上面放置一个半径为5cm的小球,放置完毕以后小球顶端距离地面20cm,则该管道的直径AB为 . 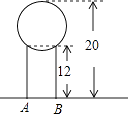
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E. 
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E是AD的中点,延长CB到点F,使![]() ,连接BE、AF.
,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.

(1)求A,B两点的坐标;
(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,问:
①若△PBO的面积为S,求S关于a的函数解析式;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;
”表示每抛两次就有一次正面朝上;
③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近,正确的说法是
附近,正确的说法是
A.①④ B.②③ C.②④ D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com