练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．分解因式：1-x4=（1+x2）（1+x）（1-x）．

    分析 原式利用平方差公式分解即可．

    解答 解：原式=（1+x2）（1-x2）=（1+x2）（1+x）（1-x）．
    故答案为：（1+x2）（1+x）（1-x）

    点评 此题考查了因式分解-运用公式法，熟练掌握平方差公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．计算：3tan30°-|-$\sqrt{3}$|-（$\frac{1}{2}$）-2+（π-3.14）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．只用下列正多边形地砖中的一种，不能镶嵌的是（　　）
    A．正三角形B．正四边形C．正五边形D．正六边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

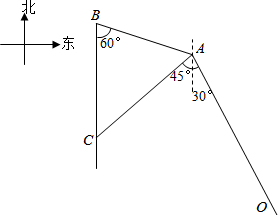    19．背景材料：近年来由于世界各国大力发展海洋经济、加强海洋能力开发，海洋争端也呈上升趋势．为增强海洋执法能力、维护海洋领土，近期我国多个部门联合进行护航、护渔演习．
    解决问题：
    （1）如图，我国渔船（C）在钓鱼岛海域正被某国不明船只袭扰，“中国海政310”船（A）接到陆地指挥中心（B）护渔命令时，渔船（C）位于陆地指挥中心正南方向，位于“中国海政310”船西南方向，“中国海政310”船位于陆地指挥中心南偏东60°方向，AB=$\frac{{140\sqrt{6}}}{3}$海里，“中国海政310”船最大航速为20海里/小时．根据以上信息，请你求出“中国海政310”船赶往渔船所在位置进行护渔至少需要多长时间？
    （2）如果（1）中条件不变，此时位于“中国海政310”船（A）南偏东30°海域有一只某国军舰（O），AO=560$\sqrt{2}$海里，其火力打击范围是500海里，如果渔船沿着正南方向继续航行，是否会驶进这只军舰的打击范围？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各式化成最简二次根式后被开方数是2的是（　　）
    A．$\sqrt{4}$B．$\sqrt{8}$C．$\sqrt{12}$D．$\sqrt{24}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

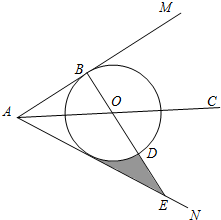    16．如图，AC平分∠MAN，点O在射线AC上，以点O为圆心，半径为1的⊙O与AM相切于点B，连接BO并延长交⊙O于点D，交AN于点E．
    （1）求证：AN是⊙O的切线；
    （2）若∠MAN=60°，求图中阴影部分的面积（结果保留根号和π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

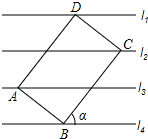    7．已知直线l1∥l2∥l3∥l4，相邻的两条平行直线间的距离均为h，矩形ABCD的四个顶点分别在这四条直线上，放置方式如图所示，AB=6，BC=8，则tanα的值等于（　　）
    A．2：3B．3：4C．4：3D．3：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．【问题情境】如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．
    【结论运用】如图2，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；
    【迁移拓展】图3是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，
    ED⊥AD，EC⊥CB，垂足分别为D、C，且AD•CE=DE•BC，AB=8，AD=3，BD=7；M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解方程组：$\left\{\begin{array}{l}{x-y-z=5}\\{y-z-x=1}\\{z-x-y=-15}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案