练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，点D是AC上一点，添加下列哪个条件不能得到△CBD∽△CAB的是（ ）

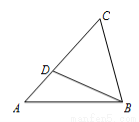
    A．∠CDB=∠CBA B．∠CBD=∠A C．BC·AB =BD·AC D．BC2=CD·AC

    C．

    【解析】

    试题分析：A．∵∠C=∠C，∠CDB=∠CBA，∴△CBD∽△CAB，故本选项错误；

    B．∵∠C=∠C，∠CBD=∠A，∴△CBD∽△CAB，故本选项错误；

    C．∵∠C=∠C，BC•AB=BD•AC不是对应边，∴不能判定△CBD∽△CAB，故本选项正确；

    D．∵∠C=∠C，BC2=CD•AC，∴△CBD∽△CAB，故本选项错误．

    故选C．

    考点：相似三角形的判定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年山东省新泰市九年级上学期片区竞赛数学试卷（解析版） 题型：选择题

    如图，直线l和双曲线y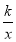＝ (k>0)交于A，B两点，P是线段AB上的点(不与A，B重合)，过点A，B，P分别向x轴作垂线，垂足分别是C，D，E，连接OA，OB，OP，设△AOC面积是S1，△BOD面积是S2，△POE面积是S3，则( ).

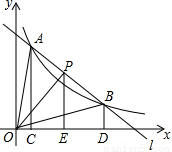
    A．S1＜S2＜S3 B．S1>S2>S3 C．S1＝S2>S3 D．S1＝S2<S3

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省九年级上学期12月月考数学试卷（解析版） 题型：选择题

    抛物线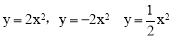共有的性质是（ ）

    A．开口向下 B．对称轴是y轴

    C．都有最低点 D．y随x的增大而减小

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省射阳县九年级上学期期末考试数学试卷（解析版） 题型：填空题

    已知二次函数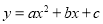的图像过点A（1，2），B（3，2），C（5，7）．若点M（－2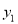，），N（－1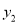，），K（8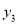，）也在二次函数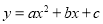的图像上，则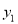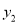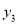，，的从小到大的关系是 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省射阳县九年级上学期期末考试数学试卷（解析版） 题型：填空题

    截至2013年12月31日，余额宝规模已达到1853亿元，这个数据用科学记数法可表示为 元．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷（解析版） 题型：解答题

    （本题满分12分）问题提出：平面内不在同一条直线上的三点确定一个圆．那么平面内的四点(任意三点均不在同一直线上），能否在同一个圆呢？

    初步思考：设不在同一条直线上的三点A、B、C确定的圆为⊙O．

    ⑴当C、D在线段AB的同侧时，

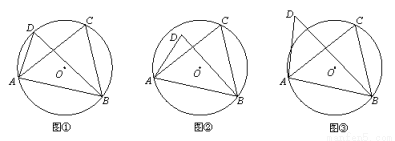
    如图①，若点D在⊙O上，此时有∠ACB＝∠ADB，理由是 ；

    如图②，若点D在⊙O内，此时有∠ACB ∠ADB；

    如图③，若点D在⊙O外，此时有∠ACB ∠ADB．（填“＝”、“＞”或“＜”）；

    由上面的探究，请直接写出A、B、C、D四点在同一个圆上的条件： ．

    类比学习：（2）仿照上面的探究思路，请探究：当C、D在线段AB的异侧时的情形．

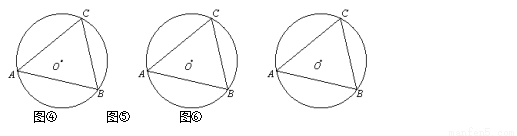
    如图④，此时有 ，

    如图⑤，此时有 ，

    如图⑥，此时有 ．

    由上面的探究，请用文字语言直接写出A、B、C、D四点在同一个圆上的条件：

    ．

    拓展延伸：（3）如何过圆上一点，仅用没有刻度的直尺，作出已知直径的垂线？

    已知：如图，AB是⊙O的直径，点C在⊙O上．

    求作：CN⊥AB．

    作法：①连接CA， CB；

    ②在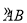上任取异于B、C的一点D，连接DA，DB；

    ③DA与CB相交于E点，延长AC、BD，交于F点；

    ④连接F、E并延长，交直径AB于M；

    ⑤连接D、M并延长，交⊙O于N．连接CN． 则CN⊥AB．

    请按上述作法在图④中作图，并说明CN⊥AB的理由．（提示：可以利用（2）中的结论）

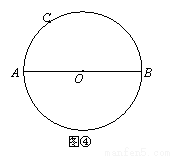
    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷（解析版） 题型：解答题

    （本题满分8分）九（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：

    甲

    7

    8

    9

    7

    10

    10

    9

    10

    10

    10

    乙

    10

    8

    7

    9

    8

    10

    10

    9

    10

    9

    （1）甲队成绩的中位数是 分，乙队成绩的众数是 分；

    （2）计算乙队的平均成绩和方差；

    （3）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是 队．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷（解析版） 题型：选择题

    把抛物线y = ?x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（ ）

    A．y = ?(x ? 1)2 ? 3 B．y = ?(x + 1)2 + 3

    C．y = ?(x ? 1)2 + 3 D．y = ?(x + 1)2 ? 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直线y = kx + b如图所示，则下列结论①k＞0，②b＞0，③k+b＞0，④2k+b=0，其中正确的结论是                （填序号）

     


    查看答案和解析>>

    同步练习册答案