
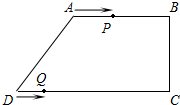
 如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).
如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).分析 (1)过点A作AM⊥CD于M,根据勾股定理,可以求出DM=6所以DC=16.
(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图示,由题可得:BP=10-3t,DQ=2t,所以可以列出方程10-3t=2t,解得t=2,此时,BP=DQ=4,CQ=12,在△CBQ中,根据勾股定理,求出BQ即可.
(3)此题要分三种情况进行讨论:即①当点P在线段AB上,②当点P在线段BC上,③当点P在线段CD上,根据三种情况点的位置,可以确定t的值.
解答  解:(1)如图1,过点A作AM⊥CD于M,
解:(1)如图1,过点A作AM⊥CD于M,
根据勾股定理,AD=10,AM=BC=8,
∴DM=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴CD=16;
(2)当四边形PBQD为平行四边形时,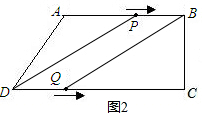
点P在AB上,点Q在DC上,如图2,
由题知:BP=10-3t,DQ=2t
∴10-3t=2t,解得t=2
此时,BP=DQ=4,CQ=12
∴BQ=$\sqrt{{8}^{2}+1{2}^{2}}$=4$\sqrt{13}$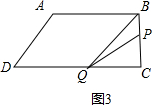
∴四边形PBQD的周长=2(BP+BQ)=8+8$\sqrt{13}$;
(3)①当点P在线段BC上时,即$\frac{10}{3}$<t≤6时,如图3,
BP=3t-10,CQ=16-2t
∴S△BPQ=$\frac{1}{2}$BP•CQ=$\frac{1}{2}$(3t-10)×(16-2t)=16,
解得:t=6,或t=$\frac{16}{3}$;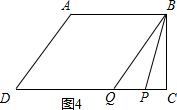
②如图4,当点P在线段CD上时,
若点P在Q的右侧,即6≤t≤$\frac{34}{5}$,
则有PQ=34-5t,S△BPQ=$\frac{1}{2}$(34-5t)×8=16,
解得:t=6,
若点P在Q的左侧,
即$\frac{34}{5}$<t≤8,
则有PQ=5t-34,S△BPQ=$\frac{1}{2}$(5t-34)×8=16,
解得t=7.6,
综合得,满足条件的t存在,其值分别为t=6,或t=$\frac{16}{3}$,或t=7.6.
点评 此题主要考查了四边形综合应用以及勾股定理和平行四边形的性质以及直角梯形的性质等知识,熟练利用平行四边形性质得出BP=DQ是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
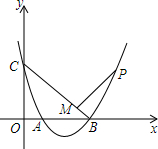 如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.
如图,抛物线y=x2-3x+2与坐标轴交于A、B、C三点,点P为抛物线上一点,PM⊥BC于M,且$\frac{PM}{CM}$=$\frac{1}{2}$,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=8}\\{10(x+y)+18=yx}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
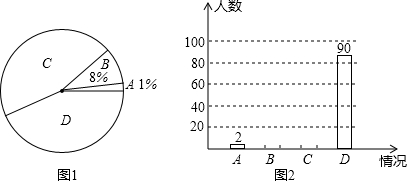
 某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com