
 如图所示,在锐角△ABC中,高CD、BE相交于点F.
如图所示,在锐角△ABC中,高CD、BE相交于点F.分析 (1)根据垂直的定义得到∠AEB=∠ADC=90°,根据有两组角对应相等的两个三角形相似证明结论;
(2)根据∠AEB=∠ADC=90°,得到E、D、B、C四点共圆,根据圆内接四边形的性质得到∠ADE=∠ACB,证明结论.
解答 解:(1)△AEB∽△ADC,△CFE∽△BFD;
∵BE⊥AC,CD⊥AB,
∴∠AEB=∠ADC=90°,
又∵∠A=∠A,
∴△AEB∽△ADC;
(2)∵∠AEB=∠ADC=90°,
∴E、D、B、C四点共圆,
∴∠ADE=∠ACB,
又∵∠A=∠A,
∴△ADE∽△ACB.
点评 本题考查的是相似三角形的判定,掌握有两组角对应相等的两个三角形相似是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:解答题
已知:如图,P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足分别为C、D。
求证:(1)OC=OD
(2)OP是CD的垂直平分线.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年广西南宁市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
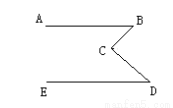
如图所示,AB∥ED,∠B=48º,∠D=42º,BC垂直于CD吗?如果垂直请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).
某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com