
【题目】如图,在![]() △
△![]() 中,
中,![]() ,
,![]() ;若将△
;若将△![]() 绕点
绕点![]() 逆时针旋转60°到△
逆时针旋转60°到△![]() 的位置,连接
的位置,连接![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接AA′,延长AC′交A′B于点D,易证:A′BA是等边三角形,得AB=A′B=A′A=2![]() ,易证:A′AC′BAC′,从而得∠A′AC′=∠BAC′,AD⊥A′B,A′D=BD=
,易证:A′AC′BAC′,从而得∠A′AC′=∠BAC′,AD⊥A′B,A′D=BD=![]() =
=![]() ,由勾股定理可得:AD,C′D的值,进而求出答案.
,由勾股定理可得:AD,C′D的值,进而求出答案.
将△![]() 绕点
绕点![]() 逆时针旋转60°到△
逆时针旋转60°到△![]() 的位置,连接AA′,延长AC′交A′B于点D.
的位置,连接AA′,延长AC′交A′B于点D.
∵A′B=AB,∠A′BA=60°,
∴A′BA是等边三角形,
∵在![]() △
△![]() 中,
中,![]() ,
,![]() ,
,
∴AB=A′B=A′A=2![]() ,
,
在A′AC′和BAC′中,
∵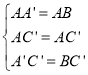 ,
,
∴A′AC′≌BAC′(SSS),
∴∠A′AC′=∠BAC′,
∴AD⊥A′B,A′D=BD=![]() =
=![]() ,
,
∴![]() ,
,
![]() ,
,
∴C′A=AD-C′D=![]() .
.
故选B.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:方案一所示图形是顶点在原点的抛物线的一部分,方案二所示图形是射线.其中![]() (件)表示推销员推销产品的数量,
(件)表示推销员推销产品的数量,![]() (元)表示付给推销员的月报酬.
(元)表示付给推销员的月报酬.
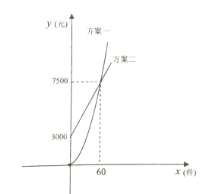
(1)分别求两种方案中![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当推销员推销产品的数量达到多少件时,两种方案月报酬差额将达到![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理.如图,若a=4,b=6,则该直角三角形的周长为( )
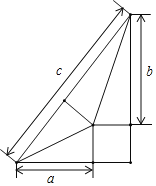
A.18B.20C.24D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
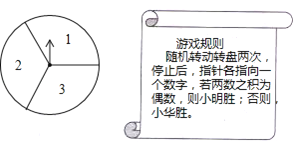
(1)现随机转动转盘一次,停止后,指针指向2的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
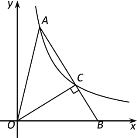
【题目】如图,在平面直角坐标系中,O为原点,点A在第一象限,点B是x轴正半轴上一点,∠OAB![]() 45°,双曲线
45°,双曲线![]() 过点A,交AB于点C,连接OC,若OC⊥AB,则tan∠ABO的值是_____.
过点A,交AB于点C,连接OC,若OC⊥AB,则tan∠ABO的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
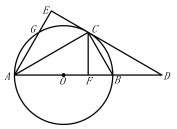
【题目】已知⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() 交
交![]() 的延长线于
的延长线于![]() ,交⊙
,交⊙![]() 于
于![]() ,
,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 的中点.
的中点.
⑴求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑵若![]() 是一元二次方程
是一元二次方程![]() 的两根,求
的两根,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
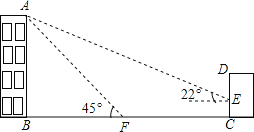
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
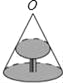
【题目】如图是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
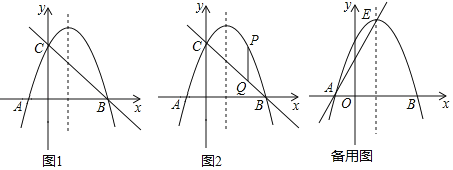
【题目】如图1,抛物线y=﹣x2+2x+3的图象与x轴交于点A、B,与y轴交于点C,连接BC.
(1)求直线BC的解析式;
(2)如图2,点P是抛物线在第一象限内的一点,作PQ∥y轴交BC于Q,当线段PQ的长度最大时,在x轴上找一点M,使PM+CM的值最小,求PM+CM的最小值;
(3)抛物线的顶点为点E,连接AE,在抛物线上是否存在一点N,使得直线AN与直线AE的夹角为45度,若存在请直接写出满足条件的点N的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com