
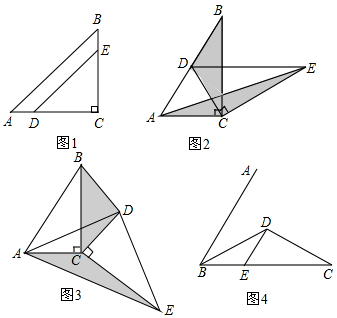
ЗжЮі ЃЈ1ЃЉЂйгЩЁїDECШЦЕуCа§зЊЕуDЧЁКУТфдкABБпЩЯЃЌЕУЕНAC=CDЃЌЭЦГіЁїACDЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУЕНЁЯACD=45ЁуЃЌЕШСПДњЛЛЕУЕНЁЯACD=ЁЯCDEЃЌИљОнЦНааЯпЕФХаЖЈЖЈРэМДПЩЕУЕННсТлЃЛЂкИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕНCD=AC=$\frac{1}{2}$ABЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌЁїADCЕФБпACЩЯЕФИпЪЧ$\frac{1}{2}$ACЃЌЧѓЕУЁїBDCЕФУцЛ§КЭЁїAECЕФУцЛ§ЯрЕШЃЈЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШЃЉЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉИљОна§зЊЕФаджЪПЩЕУBC=CEЃЌAC=CDЃЌдйЧѓГіЁЯACN=ЁЯDCMЃЌШЛКѓРћгУЁАНЧНЧБпЁБжЄУїЁїACNКЭЁїDCMШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУAN=DMЃЌШЛКѓРћгУЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШжЄУїЃЛ
ЃЈ3ЃЉЙ§ЕуDзїDF1ЁЮBEЃЌЧѓГіЫФБпаЮBEDF1ЪЧСтаЮЃЌИљОнСтаЮЕФЖдБпЯрЕШПЩЕУBE=DF1ЃЌШЛКѓИљОнЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШПЩжЊЕуF1ЮЊЫљЧѓЕФЕуЃЌЙ§ЕуDзїDF2ЁЭBDЃЌЧѓГіЁЯF1DF2=60ЁуЃЌДгЖјЕУЕНЁїDF1F2ЪЧЕШБпШ§НЧаЮЃЌШЛКѓЧѓГіDF1=DF2ЃЌдйЧѓГіЁЯCDF1=ЁЯCDF2ЃЌРћгУЁАБпНЧБпЁБжЄУїЁїCDF1КЭЁїCDF2ШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЕФУцЛ§ЯрЕШПЩЕУЕуF2вВЪЧЫљЧѓЕФЕуЃЌШЛКѓдкЕШбќЁїBDEжаЧѓГіBEЕФГЄЃЌМДПЩЕУНтЃЎ
НтД№ НтЃКЃЈ1ЃЉЂйЁпЁїDECШЦЕуCа§зЊЕуDЧЁКУТфдкABБпЩЯЃЌ
ЁрAC=CDЃЌ
ЁпЁЯBAC=90Ёу-ЁЯB=90Ёу-45Ёу=45ЁуЃЌ
ЁрЁїACDЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯACD=45ЁуЃЌ
гжЁпЁЯCDE=ЁЯBAC=45ЁуЃЌ
ЁрЁЯACD=ЁЯCDEЃЌ
ЁрDEЁЮACЃЛ
ЂкЁпЁЯB=45ЁуЃЌЁЯC=90ЁуЃЌ
ЁрCD=AC=$\frac{1}{2}$ABЃЌ
ЁрBD=AD=CD=$\frac{\sqrt{2}}{2}$ACЃЌ
ИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌЁїADCЕФБпACЩЯЕФИпЪЧ$\frac{1}{2}$ACЃЌ
ЁрЁїBDCЕФУцЛ§=$\frac{1}{2}$BD•CD=$\frac{1}{2}$ЁС$\frac{\sqrt{2}}{2}$AC•$\frac{\sqrt{2}}{2}$AC=$\frac{1}{4}$AC2ЃЌЁїAECЕФУцЛ§=$\frac{1}{2}$AC•$\frac{1}{2}$AC=$\frac{1}{4}$AC2ЃЌ
ЁрЁрЁїBDCЕФУцЛ§КЭЁїAECЕФУцЛ§ЯрЕШЃЈЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШЃЉЃЌ
МДS1=S2ЃЛ
ЙЪД№АИЮЊЃКDEЁЮACЃЛS1=S2ЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌЁпЁїDECЪЧгЩЁїABCШЦЕуCа§зЊЕУЕНЃЌ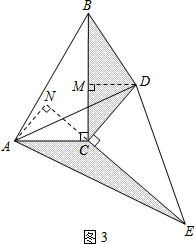
ЁрBC=CEЃЌAC=CDЃЌ
ЁпЁЯACN+ЁЯBCN=90ЁуЃЌЁЯDCM+ЁЯBCN=180Ёу-90Ёу=90ЁуЃЌ
ЁрЁЯACN=ЁЯDCMЃЌ
ЁпдкЁїACNКЭЁїDCMжаЃЌ
$\left\{\begin{array}{l}{ЁЯACN=ЁЯDCM}\\{ЁЯCMD=ЁЯN=90Ёу}\\{AC=CD}\end{array}\right.$ЃЌ
ЁрЁїACNЁеЁїDCMЃЈAASЃЉЃЌ
ЁрAN=DMЃЌ
ЁрЁїBDCЕФУцЛ§КЭЁїAECЕФУцЛ§ЯрЕШЃЈЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШЃЉЃЌ
МДS1=S2ЃЛ
ЃЈ3ЃЉШчЭМ4ЃЌЙ§ЕуDзїDF1ЁЮBEЃЌвзЧѓЫФБпаЮBEDF1ЪЧСтаЮЃЌ
ЫљвдBE=DF1ЃЌЧвBEЁЂDF1ЩЯЕФИпЯрЕШЃЌ
ДЫЪБSЁїDCF1=SЁїBDEЃЛ
Й§ЕуDзїDF2ЁЭBDЃЌ
ЁпЁЯABC=60ЁуЃЌF1DЁЮBEЃЌ
ЁрЁЯF2F1D=ЁЯABC=60ЁуЃЌ
ЁпBF1=DF1ЃЌЁЯF1BD=$\frac{1}{2}$ЁЯABC=30ЁуЃЌЁЯF2DB=90ЁуЃЌ
ЁрЁЯF1DF2=ЁЯABC=60ЁуЃЌ
ЁрЁїDF1F2ЪЧЕШБпШ§НЧаЮЃЌ
ЁрDF1=DF2ЃЌ
ЁпBD=CDЃЌЁЯABC=60ЁуЃЌЕуDЪЧНЧЦНЗжЯпЩЯвЛЕуЃЌ
ЁрЁЯDBC=ЁЯDCB=$\frac{1}{2}$ЁС60Ёу=30ЁуЃЌ
ЁрЁЯCDF1=180Ёу-ЁЯBCD=180Ёу-30Ёу=150ЁуЃЌ
ЁЯCDF2=360Ёу-150Ёу-60Ёу=150ЁуЃЌ
ЁрЁЯCDF1=ЁЯCDF2ЃЌ
ЁпдкЁїCDF1КЭЁїCDF2жаЃЌ
$\left\{\begin{array}{l}{D{F}_{1}=D{F}_{2}}\\{ЁЯCD{F}_{1}=ЁЯCD{F}_{2}}\\{CD=CD}\end{array}\right.$ЃЌ
ЁрЁїCDF1ЁеЁїCDF2ЃЈSASЃЉЃЌ
ЁрЕуF2вВЪЧЫљЧѓЕФЕуЃЌ
ЁпЁЯABC=60ЁуЃЌЕуDЪЧНЧЦНЗжЯпЩЯвЛЕуЃЌDEЁЮABЃЌ
ЁрЁЯDBC=ЁЯBDE=ЁЯABD=$\frac{1}{2}$ЁС60Ёу=30ЁуЃЌ
гжЁпBD=4ЃЌ
ЁрBE=$\frac{1}{2}$ЁС4ЁТcos30Ёу=2ЁТ$\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$ЃЌ
ЁрBF1=$\frac{4\sqrt{3}}{3}$ЃЌBF2=BF1+F1F2=$\frac{4\sqrt{3}}{3}$+$\frac{4\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$ЃЌ
ЙЪBFЕФГЄЮЊ$\frac{4\sqrt{3}}{3}$Лђ$\frac{8\sqrt{3}}{3}$ЃЎ
ЕуЦР БОЬтПМВщСЫШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪЃЌШ§НЧаЮЕФУцЛ§ЃЌЕШБпШ§НЧаЮЕФХаЖЈгыаджЪЃЌжБНЧШ§НЧаЮ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЕФаджЪЃЌЪьСЗеЦЮеЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШЃЌвдМАШЋЕШШ§НЧаЮЕФУцЛ§ЯрЕШЪЧНтЬтЕФЙиМќЃЌЃЈ3ЃЉвЊзЂвтЗћКЯЬѕМўЕФЕуFгаСНИіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
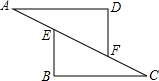 ШчЭМЃЌвбжЊЕуAЁЂEЁЂFЁЂCдкЭЌвЛжБЯпЩЯЃЌAE=FCЃЌЙ§ЕуAЁЂC зїADЁЮBCЃЌЧвAD=CBЃЎ
ШчЭМЃЌвбжЊЕуAЁЂEЁЂFЁЂCдкЭЌвЛжБЯпЩЯЃЌAE=FCЃЌЙ§ЕуAЁЂC зїADЁЮBCЃЌЧвAD=CBЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌЯТСаЭМжааЁе§ЗНаЮЕФБпГЄЮЊ1ЃЌвѕгАШ§НЧаЮЕФЖЅЕуОљдкИёЕуЩЯЃЌгыЁїABCЯрЫЦЕФЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌЯТСаЭМжааЁе§ЗНаЮЕФБпГЄЮЊ1ЃЌвѕгАШ§НЧаЮЕФЖЅЕуОљдкИёЕуЩЯЃЌгыЁїABCЯрЫЦЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ |  | BЃЎ | 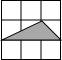 | CЃЎ |  | DЃЎ | 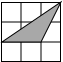 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
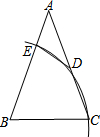 ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯA=36ЁуЃЌвдBЮЊдВаФЃЌBCЮЊАыОЖзїЛЁЃЌЗжБ№НЛACЁЂABгкЕуDЁЂEЃЌСЌНгDEЃЌдђЁЯADE=36ЁуЃЎ
ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯA=36ЁуЃЌвдBЮЊдВаФЃЌBCЮЊАыОЖзїЛЁЃЌЗжБ№НЛACЁЂABгкЕуDЁЂEЃЌСЌНгDEЃЌдђЁЯADE=36ЁуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{5}{4}$ | BЃЎ | $\frac{4}{5}$ | CЃЎ | $\frac{3}{4}$ | DЃЎ | $\frac{4}{3}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
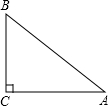 ШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯA=40ЁуЃЌдђЁЯB=50ЁуЃЎ
ШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯA=40ЁуЃЌдђЁЯB=50ЁуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 5$\sqrt{3}$-2$\sqrt{3}$=3 | BЃЎ | 2$\sqrt{2}$ЁС3$\sqrt{2}$=6$\sqrt{2}$ | CЃЎ | $\sqrt{3}+2\sqrt{3}$=3 | DЃЎ | 3$\sqrt{3}$$ЁТ\sqrt{3}$=3 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com