
分析 问题1:根据阅读2得到x+$\frac{4}{x}$的范围,进一步得到周长的最小值;
问题2:将$\frac{{y}_{2}}{{y}_{1}}$变形为(x+1)+$\frac{9}{x+1}$,根据阅读2得到(x+1)+$\frac{9}{x+1}$,的范围,进一步即可求解;
问题3:可设学校学生人数为x人,根据生均投入=支出总费用÷学生人数,列出代数式,再根据阅读2得到范围,从而求解.
解答 解:问题1:x=$\frac{4}{x}$(x>0),解得x=2,
x=2时,x+$\frac{4}{x}$有最小值为2×$\sqrt{4}$=4.
故当x=2时,周长的最小值为2×4=8.
问题2:∵函数y1=x+1(x>-1),函数y2=x2+2x+10(x>-1),
∴$\frac{{y}_{2}}{{y}_{1}}$=(x+1)+$\frac{9}{x+1}$,
x+1=$\frac{9}{x+1}$,解得x=2,
x=2时,(x+1)+$\frac{9}{x+1}$有最小值为2×$\sqrt{9}$=6.
问题3:设学校学生人数为x人,
则生均投入=$\frac{4900+10x+0.01{x}^{2}}{x}$=10+0.01x+$\frac{4900}{x}$=10+0.01(x+$\frac{490000}{x}$),
x=$\frac{490000}{x}$(x>0),解得x=700,
x=700时,x+$\frac{490000}{x}$有最小值为2×$\sqrt{490000}$=1400,
故当x=700时,生均投入的最小值为10+0.01×1400=24元.
答:当学校学生人数为700时,该校每天生均投入最低,最低费用是24元.
故答案为:2,8;2,6.
点评 考查了二次函数的应用,本题关键是理解阅读1和阅读2的知识点:当x=$\frac{m}{x}$,即x=$\sqrt{m}$时,函数y=x+$\frac{m}{x}$的最小值为2$\sqrt{m}$.


科目:初中数学 来源: 题型:选择题
| A. | 0.113×105 | B. | 1.13×104 | C. | 11.3×103 | D. | 113×102 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
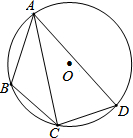 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.
如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.34×102 | B. | 1.34×103 | C. | 1.34×104 | D. | 1.34×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
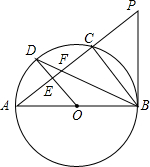 已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com