
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 利用二次根式的性质对(1)进行判断;根据积的乘方与幂的乘方和同底数幂的乘法对(2)进行判断;利用分母有理化对(4)进行判断;根据平方差公式对(5)进行判断.
解答 解:$\sqrt{(-5)^{2}}$=5,所以(1)正确;
(-2x2y3)2(xy)3=4x4y6•x3y3=4x7y9,所以(2)正确;
(3)$\frac{\sqrt{16}-2}{\sqrt{3}+1}$=$\frac{4-2}{\sqrt{3}+1}$=$\frac{2}{\sqrt{3}+1}$=$\sqrt{3}$-1,所以(3)正确;
(4)$\frac{xy-{x}^{2}}{(x-y)^{2}}$=$\frac{-x(x-y)}{(x-y)^{2}}$=$\frac{x}{y-x}$,所以(4)正确;
(5)(x+y-z)(x+y+z)=(x+y)2-z2.所以(5)正确.
故选D.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了整式的运算.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.
如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
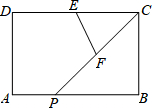 如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.
如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
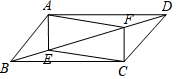 如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.
如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
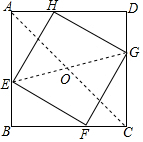 如图,正方形ABCD的边长为10cm,E,F,G,H分别是AB,BC,CD,DA上的点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为10cm,E,F,G,H分别是AB,BC,CD,DA上的点,且AE=BF=CG=DH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
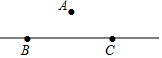 如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)
如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com