
【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法,例如:
①用配方法分解因式:![]() .
.
解:原式![]()
②![]() ,利用配方法求
,利用配方法求![]() 的最小值.
的最小值.
解:![]()
∵![]() ,
,![]()
∴当![]() 时,
时,![]() 有最小值1.
有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]() ________.
________.
(2)用配方法因式分解:![]() .
.
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
(4)已知![]() ,则
,则![]() 的值为________.
的值为________.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料后完成.
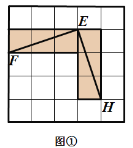
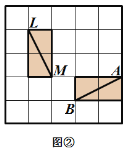
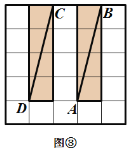
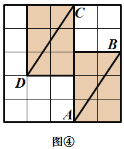
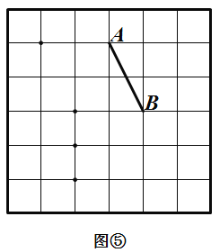
有这样一个游戏,游戏规则如下所述:如图①—图④,都是边 长为![]() 的
的![]() 网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知
网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知![]() .在图③ 和图④中,可知
.在图③ 和图④中,可知![]() . 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的
. 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的![]() 网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段
网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段![]() 垂直 的线段(或者直线)
垂直 的线段(或者直线)![]() ,再画出与线段
,再画出与线段![]() 平行的一条线段(或者 直线)
平行的一条线段(或者 直线)![]() . 第二关:在图⑥的
. 第二关:在图⑥的![]() 网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)
网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC在整个平移过程中线段AC扫过的面积为________.
(3)能使S△MBC=S△ABC的格点M共有_______个(点M异于点A)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,
,![]() 为垂足,
为垂足,![]() 的平分线交直线
的平分线交直线![]() 于点
于点![]() ,回答下列问题并说明.(可在图上标注数字角)
,回答下列问题并说明.(可在图上标注数字角)
(1)如图①,![]() 为边
为边![]() 上一点,则
上一点,则![]() 、
、![]() 的位置关系是________.请给予证明;
的位置关系是________.请给予证明;

(2)如图②,![]() 为边
为边![]() 反向延长线上一点,则
反向延长线上一点,则![]() 、
、![]() 的位置关系是________.(请直接写出结论)
的位置关系是________.(请直接写出结论)

(3)如图③,![]() 为边
为边![]() 延长线上一点,则
延长线上一点,则![]() 、
、![]() 的位置关系是________.请给予证明.
的位置关系是________.请给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD
S菱形ABCD
下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为![]() ,
,![]() ,
,![]() ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形![]() .
.
(1)画出三角形ABC和平移后![]() 的图形;
的图形;
(2)写出三个顶点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表中的二次函数 ![]() 的自变量x与函数y的对应值,可判断二次函数的图像与x轴( )
的自变量x与函数y的对应值,可判断二次函数的图像与x轴( )
A.只有一个交点
B.有两个交点,且它们分别在y轴两侧
C.有两个交点,且它们均在y轴同侧
D.无交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com