
 如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )| A. | 50 | B. | 45 | C. | 40 | D. | 35 |
分析 过P作PN⊥AB于N,交EF于Q,同样也垂直于CD,利用相似三角形的性质可求出NP,PQ,以及EF的长,再利用三角形的面积公式可求出△ABP和△EFP的面积,用矩形ABCD的面积减去△ABP的面积减去△EFP的面积,即可求阴影部分面积.
解答 解:过作PN⊥AB于N,交EF于Q,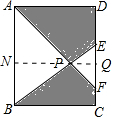
∵△EFP∽△BAP,相似比是EF:AB=1:2,
∴PN:PQ=AB:EF=2:1,
又∵NQ=BC=6,
∴PN=4,PQ=2,
∴S△ABP=$\frac{1}{2}$×10×4=20,
∴S△EFP=$\frac{1}{2}$×5×2=5,S矩形ABCD=6×10=60,
∴S阴影=60-20-5=35.
故选D.
点评 本题主要考查了相似三角形的性质,求出阴影部分的面积可以转化为几个规则图形的面积的和或差的关系.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:选择题
 某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为( )人.
某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为( )人.| A. | 120 | B. | 110 | C. | 100 | D. | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
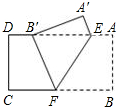 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{180-x}{x}$-$\frac{180-x}{1.5x}$=40 | B. | $\frac{180-x}{x}$-$\frac{180-x}{1.5x}$=$\frac{40}{60}$ | ||
| C. | $\frac{180}{x}$-$\frac{180}{1.5x}$=40 | D. | $\frac{180}{x}$-$\frac{180}{1.5x}$=$\frac{40}{60}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
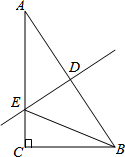 如图,Rt△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为( )
如图,Rt△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com