
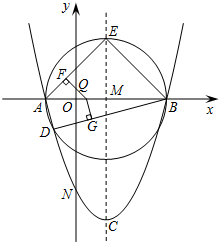
 如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.分析 (1)证明相似,思路很常规,就是两个角相等或边长成比例.因为题中由圆周角易知一对相等的角,那么另一对角相等就是我们需要努力的方向,因为涉及圆,倾向于找接近圆的角∠DPF,利用补角在圆内作等量代换,等弧对等角等知识易得∠DPF=∠APC,则结论易证.
(2)求PD的长,且此线段在上问已证相似的△PDF中,很明显用相似得成比例,再将其他边代入是应有的思路.利用已知条件易得其他边长,则PD可求.
(3)因为题目涉及∠AFD与也在第一问所得相似的△PDF中,进而考虑转化,∠AFD=∠PCA,连接PB得∠AFD=∠PCA=∠PBG,过G点作AB的垂线,若此线过PB与AC的交点那么结论易求,因为根据三角函数或三角形与三角形ABC相似可用AG表示∠PBG所对的这条高线.但是“此线是否过PB与AC的交点”?此时首先需要做的是多画几个动点P,观察我们的猜想.验证得我们的猜想应是正确的,可是证明不能靠画图,如何求证此线过PB与AC的交点是我们解题的关键.常规作法不易得此结论,我们可以换另外的辅助线作法,先做垂线,得交点H,然后连接交点与B,再证明∠HBG=∠PCA=∠AFD.因为C、D关于AB对称,可以延长CG考虑P点的对称点.根据等弧对等角,可得∠HBG=∠PCA,进而得解题思路.
解答 解:(1)∵四边形APCB内接于圆O,
∴∠FPC=∠B.
又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,
∴∠APD=∠FPC,∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD,
又∵∠PAC=∠PDC,
∴△PAC∽△PDF;
(2)如图1,连接PO,则由$\widehat{AP}$=$\widehat{BP}$,有PO⊥AB,且∠PAB=45°,△APO、△AEF都为等腰直角三角形. 在Rt△ABC中,
在Rt△ABC中,
∵tan∠CAB=$\frac{1}{2}$,
∴AC=2BC,
∴AB2=BC2+AC2=5BC2,
∵AB=5,
∴BC=$\sqrt{5}$,
∴AC=2$\sqrt{5}$,
∴CE=AC•sin∠BAC=AC•$\frac{BC}{AB}$=2$\sqrt{5}$•$\frac{\sqrt{5}}{5}$=2,
AE=AC•cos∠BAC=AC•$\frac{AC}{AB}$=2$\sqrt{5}$•$\frac{2\sqrt{5}}{5}$=4,
∵△AEF为等腰直角三角形,
∴EF=AE=4,
∴FD=FC+CD=(EF-CE)+2CE=EF+CE=4+2=6.
∵△APO为等腰直角三角形,AO=$\frac{1}{2}$•AB=$\frac{5}{2}$,
∴AP=$\frac{5\sqrt{2}}{2}$.
∵△PDF∽△PAC,
∴$\frac{PD}{FD}$=$\frac{PA}{CA}$,
∴$\frac{PD}{6}$=$\frac{\frac{5\sqrt{2}}{2}}{2\sqrt{5}}$,
∴PD=$\frac{3\sqrt{10}}{2}$.
(3)如图2,过点G作GH⊥AB,交AC于H,连接HB,以HB为直径作圆,连接CG并延长交⊙O于Q,
∵HC⊥CB,GH⊥GB,
∴C、G都在以HB为直径的圆上,
∴∠HBG=∠ACQ,
∵C、D关于AB对称,G在AB上,
∴Q、P关于AB对称,
∴$\widehat{AP}$=$\widehat{AQ}$,
∴∠PCA=∠ACQ,
∴∠HBG=∠PCA.
∵△PAC∽△PDF,
∴∠PCA=∠PFD=∠AFD,
∴y=tan∠AFD=tan∠PCA=tan∠HBG=$\frac{HG}{BG}$.
∵HG=tan∠HAG•AG=tan∠BAC•AG=$\frac{BC}{AC}$•AG=$\frac{1}{2}$•AG,
∴y=$\frac{1}{2}$•$\frac{AG}{BG}$=$\frac{1}{2}$x.
点评 本题考查的是圆的综合题,涉及到圆周角、相似三角形、三角函数等性质,前两问思路还算简单,但最后一问需要熟练的解题技巧需要长久的磨练总结.总体来讲本题偏难,学生练习时加强理解,重点理解分析过程,自己如何找到思路.


科目:初中数学 来源: 题型:解答题
 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
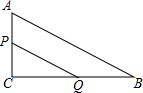 如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )
如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )| A. | 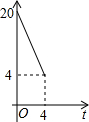 | B. | 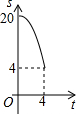 | C. | 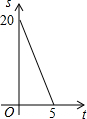 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:
如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
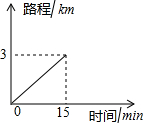 小丽家离学校2km,步行到校需30min,小丽的同学小军上学要经过小丽家,小军骑车上学行驶的路程与时间的关系如图所示.
小丽家离学校2km,步行到校需30min,小丽的同学小军上学要经过小丽家,小军骑车上学行驶的路程与时间的关系如图所示. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com