
 已知函数C1:y=kx2+($\frac{4}{3}$-3k)x-4.
已知函数C1:y=kx2+($\frac{4}{3}$-3k)x-4.分析 (1)分类讨论:①当k=0时,函数为一次函数,与x轴必有一个交点;②当k≠0时,计算判别式得到△=(3k+$\frac{4}{3}$)2≥0,由此得出无论k为何值,函数图象与x轴总有交点;
(2)①由(n-3,n-7)、(-n+1,n-7)是抛物线上的两个不同点,根据二次函数的对称性得出对称轴为直线x=$\frac{n-3-n+1}{2}$=-1,再根据对称轴公式得出-$\frac{\frac{4}{3}-3k}{2k}$=-1,解方程求出k的值,从而得出抛物线的表达式;
②将(n-3,n-7)代入y=$\frac{4}{15}$x2+$\frac{8}{15}$x-4,即可求出n的值;
(3)由二次函数的解析式求出A,B,C三点的坐标,得出三点中有两个定点(3,0),(0,-4),另一动点坐标为(-$\frac{4}{3k}$,0).当△ABC为等腰三角形时,分AB为底边、BC为底边、AC为底边三种情况求出另一动点坐标,进而求出k的值.
解答 (1)证明:①当k=0时,函数为一次函数,即y=$\frac{4}{3}$x-4,与x轴交于点(3,0);
②当k≠0时,函数为二次函数,
∵△=($\frac{4}{3}$-3k)2-4k×(-4)=(3k+$\frac{4}{3}$)2≥0,即△≥0,
∴与x轴有一个或两个交点;
综上可知,无论k为何值,函数图象与x轴总有交点;
(2)①当k≠0时,函数C1:y=kx2+($\frac{4}{3}$-3k)x-4为二次函数,
∵(n-3,n-7)、(-n+1,n-7)是抛物线上的两个不同点,
∴抛物线的对称轴为直线x=$\frac{n-3-n+1}{2}$=-1,
∴-$\frac{\frac{4}{3}-3k}{2k}$=-1,解得k=$\frac{4}{15}$,
∴抛物线的表达式为y=$\frac{4}{15}$x2+$\frac{8}{15}$x-4;
②∵(n-3,n-7)是抛物线y=$\frac{4}{15}$x2+$\frac{8}{15}$x-4上的点,
∴n-7=$\frac{4}{15}$(n-3)2+$\frac{8}{15}$(n-3)-4,
解得n1=$\frac{19}{4}$,n2=3;
(3)∵y=kx2+($\frac{4}{3}$-3k)x-4,
∴当y=0时,kx2+($\frac{4}{3}$-3k)x-4=0,
解得x1=3,x2=-$\frac{4}{3k}$,
∴如果设A点坐标为(3,0),那么B点坐标为(-$\frac{4}{3k}$,0).
∵x=0时,y=-4,
∴C点坐标为(0,-4).
当△ABC为等腰三角形时,B点坐标为(-3,0),(-2,0),(-$\frac{7}{6}$,0),(8,0),
当-$\frac{4}{3k}$=-3时,k=$\frac{4}{9}$;
当-$\frac{4}{3k}$=-2时,k=$\frac{2}{3}$;
当-$\frac{4}{3k}$=-$\frac{7}{6}$时,k=$\frac{8}{7}$;
当-$\frac{4}{3k}$=8时,k=-$\frac{1}{6}$.
综上所述,满足条件的实数k的值为$\frac{4}{9}$,$\frac{2}{3}$,$\frac{8}{7}$,-$\frac{1}{6}$.
点评 本题是二次函数综合题,考查了函数图象与方程的关系,二次函数的性质,二次函数图象上点的坐标特征,等腰三角形的性质等知识,综合性较强,难度适中.利用分类讨论以及方程思想是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 地球围绕太阳转 | |
| B. | 早上太阳从西方升起 | |
| C. | 一觉醒来,天气晴朗 | |
| D. | 口袋中有8个白球,从口袋中任取一球,会摸到黑球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
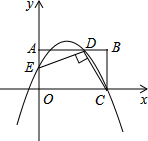 如图,平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,AD=2,连接DC,过点D作DE⊥DC交OA于点E.
如图,平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,AD=2,连接DC,过点D作DE⊥DC交OA于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC绕旋转中心(-1,0)旋转180°得到△A′B′C′,如果△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
如图,△ABC绕旋转中心(-1,0)旋转180°得到△A′B′C′,如果△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )| A. | (a-2,b) | B. | (a+2,b) | C. | (-a-2,-b) | D. | (a+2,-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
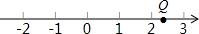 如图,数轴上的点Q所表示的数可能是( )
如图,数轴上的点Q所表示的数可能是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com