
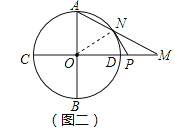
����Ŀ����ͼ����O�İ뾶Ϊ1��ֱ��CD����Բ��O������O��C��D���㣬ֱ��AB��CD����M��ֱ��CD�����ڵ�C��O��D��һ�����㣬AM���ڵ�ֱ�߽��ڡ�O�ڵ�N����P��ֱ��CD����һ�㣬��PM=PN��
��1������M�ڡ�O�ڲ�����ͼһ�����ж�PN���O�Ĺ�ϵ����д��֤�����̣�
��2������M�ڡ�O�ⲿ����ͼ����������������ʱ����1���Ľ����Ƿ�������˵�����ɣ�
��3������M�ڡ�O�ⲿ����ͼ������AMO=15������ͼ����Ӱ���ֵ������

���𰸡���1��PN���O���У�֤������������2��������֤������������3��![]()
�������������������1���������ߵ��ж��ó���PNO=��PNM+��ONA=��AMO+��ONA����������ɣ�
��2��������֪�ó���PNM+��ONA=90���������ó���PNO=180��-90��=90�����ɵó��𰸣�
��3�����ȸ�����ǵ����ʵó���AON=60�������������������ʽ�ó����ɣ�
�����������1��PN����O����
֤��������ON��

����ONA=��OAN��
��PM=PN��
���PNM=��PMN��
�ߡ�AMO=��PMN��
���PNM=��AMO��
���PNO=��PNM+��ONA=��AMO+��ONA=90����
��PN����O����
��2��������
֤��������ON��
����ONA=��OAN��
��PM=PN��
���PNM=��PMN��
��Rt��AOM����OMA+��OAM=90����
���PNM+��ONA=90����
���PNO=180��-90��=90����
��PN����O����
��3������ON��

�ɣ�2����֪��ONP=90����
�ߡ�AMO=30����PM=PN��
���PNM=30������OPN=60����
���PON=30������AON=60����
��NE��OD��������E��
��NE=ONsin30��=1��![]() =
=![]() ��
��
S��Ӱ=S��AOC+S����AON-S��CON
=![]() OCOA+
OCOA+![]() ����12-
����12-![]() CONE
CONE
=![]() ��1��1+
��1��1+![]() ��-
��-![]() ��1��
��1��![]()
=![]() +
+![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
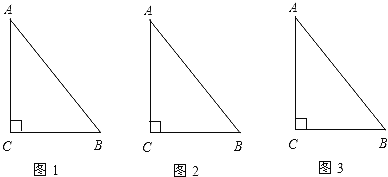
����Ŀ����һ��ֱ�������ε��̵أ�������ֱ�DZ߳��ֱ�Ϊ6m��8m������Ҫ���̵�����ɵ��������Σ������䲿������8mΪֱ�DZߵ�ֱ�������Σ������������������̵ص��ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O��ֱ��Ϊ10����A����B����C�ڡ�O�ϣ���CAB��ƽ���߽���O�ڵ�D��


��1����ͼ�٣���BCΪ��O��ֱ����AB=6����AC��BD�ij���
��2����ͼ�ڣ�����CAB=60����CF��BD������֤��CF�ǡ�O�����ߣ���������CD��CB�Լ���DBΧ��ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��ͼ���㣨4��3������3��0����
��1����b��c��ֵ��
��2������ö��κ���ͼ��Ķ�������ͶԳ��ᣬ������������ϵ�л����ú�����ͼ����
��3���ú�����ͼ��������ƽ�Ƶõ�y=x2��ͼ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC�У�AC=BC����ACB=90������D��AB���е㣬��E��AB����һ�㣮
��1��ֱ��BF��ֱ��ֱ��CE�ڵ�F����CD�ڵ�G����ͼ1������֤��AE=CG��
��2��ֱ��AH��ֱ��ֱ��CE������Ϊ��H����CD���ӳ����ڵ�M����ͼ2�����ҳ�ͼ����BE��ȵ��߶Σ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
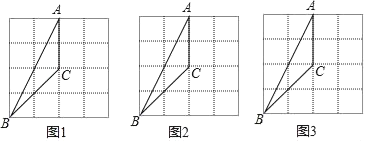
����Ŀ����ͼ����4��4�ķ���ֽ�У���ABC���������㶼�ڸ���ϣ�
��1����ͼ1�У�����һ������ABC����Գ�������ABC�й����ߵĸ�������Σ�
��2����ͼ2�У�����һ������ABC�����ĶԳƵĸ�������Σ�
��3����ͼ3�У�������ABC���ŵ�C��˳ʱ�뷽����ת90����������Σ���AB����һ��P����CP=n���������P������·���ij����ú�n����ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·MN��·PQ�ڵ�O�����㣬��QON��30��.��·PQ��A������O��240��.�������ʻʱ����Χ200�����ڻ��ܵ�������Ӱ��.��ô������·MN����ON������72ǧ�ף�ʱ���ٶ���ʻʱ��
��1��A���Ƿ���ܵ���Ӱ�죬��д������
��2�����A��������Ӱ�죬��Ӱ���ʱ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�����⣺̽��ͬһƽ��ֱ������ϵ��ϵ����Ϊ��������������������![]() ��
��![]() ��k��0����ͼ�����ʣ�
��k��0����ͼ�����ʣ�
С������ѧϰ�����ľ��飬�Ժ���![]() ��
��![]() ��k��0������k��0ʱ��ͼ�����ʽ�����̽����
��k��0������k��0ʱ��ͼ�����ʽ�����̽����
������С����̽�����̣�
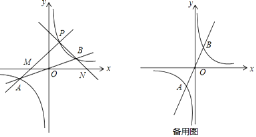
��1����ͼ��ʾ���躯��![]() ��
��![]() ͼ��Ľ���ΪA��B����֪A�������Ϊ����k����1������B�������Ϊ�� ����
ͼ��Ľ���ΪA��B����֪A�������Ϊ����k����1������B�������Ϊ�� ����
��2������PΪ��һ������˫��������ͬ�ڵ�B������һ�㣮
����ֱ��PA��x���ڵ�M��ֱ��PB��x���ڵ�N����֤��PM=PN��
֤���������£���P��m��![]() ����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
��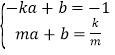 ����ã�
����ã�![]() ��
��
��ֱ��PA�Ľ���ʽΪ�� ��.
���������Ľ����̲��������������ʣ���֤����
�ڵ�P������Ϊ��1��k����k��1��ʱ���ж���PAB����״������k��ʾ����PAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڴ�����ȫ������������������ѧУ��ٰ�������֪ʶ�����𰸣�������![]() ���ֽ�Ʒ��������.�������
���ֽ�Ʒ��������.�������![]() ��25����
��25����![]() ��20��������480Ԫ���������
��20��������480Ԫ���������![]() ��15����
��15����![]() ��25��������340Ԫ.
��25��������340Ԫ.
��1��![]() ���ֽ�Ʒÿ��������Ԫ��
���ֽ�Ʒÿ��������Ԫ��
��2����Ҫ����![]() ���ֽ�Ʒ��100�����ܷ��ò�����1120Ԫ����ô����ܹ���
���ֽ�Ʒ��100�����ܷ��ò�����1120Ԫ����ô����ܹ���![]() �ֽ�Ʒ���ټ���
�ֽ�Ʒ���ټ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com