
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
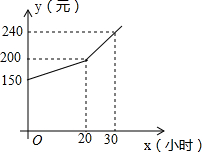 为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y元,则y(元)和x(小时)之间的函数图象如图所示.
为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y元,则y(元)和x(小时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com