练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
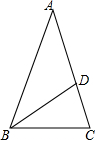
    10．如图，△ABC中，AB=AC，∠A=30°，以B为圆心，以BC为半径画弧交AC于点D，那么∠DBC的度数是（　　）
    A．30°B．45°C．40°D．60°

    分析 在△ABC中可求得∠ACB=∠ABC=75°，在△BCD中可求得∠DBC=45°，可求出∠ABD．

    解答 解：∵AB=AC，∠A=30°，
    ∴∠ABC=∠ACB=75°，
    又∵BC=BD，
    ∴∠BDC=∠BCD=75°，
    ∴∠DBC=30°，
    ∴∠ABD=∠ABC-∠DBC=75°-30°=45°，
    故选D．

    点评 本题主要考查等腰三角形的性质，掌握等边对等角是解题的关键，注意三角形内角和定理的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．已知抛物线C：y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等，且x=2时y=1，P（x，y）为抛物线C上任一点，F（0，1）为y轴上一点，PQ与直线y=-1垂直交于点Q
    （1）求出抛物线解析式；
    （2）求证：PF=PQ；
    （3）若直线y=kx+b过点F（0，1）且与抛物线C交于A、B两点，试判断以AB为直径的圆与直线y=-1位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

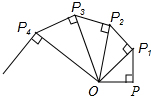    1．如图，OP=1，过P作PP1⊥OP，且PP1=1，得OP1=$\sqrt{2}$；再过P1作P1P2⊥OP1，且P1P2=1，得OP2=$\sqrt{3}$；又过P2作P2P3⊥OP2，且P2P3=1，得OP3=2；…依此法继续作下去，得OP2016=$\sqrt{2017}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．母亲节前夕，某淘宝店主从厂家购进A、B两种礼盒，已知A、B两种礼盒的单价比为2：3，单价和为200元．求A、B两种礼盒的单价分别是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，3个正方形在⊙O直径的同侧，顶点B，C，G，H都在⊙O的直径上，正方形ABCD的顶点A在⊙O上，顶点D在PC上，正方形EFGH的顶点E在⊙O上，顶点F在QG上，正方形PCGQ的顶点P也在⊙O上，若BC=1，GH=2，则正方形PCGQ的面积为（　　）
    A．5B．6C．7D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在 Rt△ABC中，∠ACB=90°，点D是边AB上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．
    （1）求证：BD=BF；
    （2）若CF=1，$\frac{OA}{BA}$=$\frac{3}{5}$，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．有理数a，b在数轴上的位置如图所示，在-a，b-a，a+b，0中，最大的是（　　）
    A．-aB．0C．a+bD．b-a

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

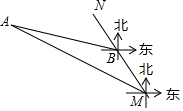    19．如图，MN表示某引水工程的一段设计路线，从点M到点N的走向为北偏西30°，在点M的北偏西60°方向上有一点A，以点A为圆心，以500米为半径的圆形区域为居民区，取MN上另一点B，测得BA的方向为北偏西75°．已知MB=400米，若不改变方向，则输水路线是否会穿过居民区？请通过计算说明理由．（参考数据：$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．在平面直角坐标系中，二次函数y=x2+ax+b的图象与x轴交于两点，且两交点之间的距离是4，若此函数图象的对称轴为x=-5，则此图象经过下列（　　）
    A．（-6，-4）B．（-6，-3）C．（-6，-2）D．（-6，-1）

    查看答案和解析>>

    同步练习册答案