
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的“三阶等腰线”.
(1)请你在图1,图2中用两种不同的方法画出顶角为36°的等腰三角形的“三阶等腰线”,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种).
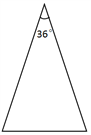



图1 图2 备用1 备用2
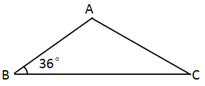
(2)△ABC中,∠B=36°,AD和DE是△ABC的“三阶等腰线”,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
【答案】(1)画图见解析;(2)满足条件的x=24或 36.
【解析】试题分析:(1)根据等腰三角形的性质和三阶等腰线的定义: ①可以作两底角角平分线, ②先作底角角平分线,再作平行线,
(2)先根据三角形内角和,等腰三角形的性质和三阶等腰线的定义,画满足要求的图形,然后根据等腰三角形的性质用x表示出三角形的内角,利用三角形内角和列出关于x的方程,解方程即可.
试题解析:(1)如图所示:
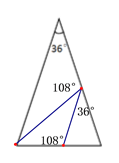
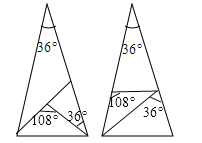
(2)①当AD=AE时,
∵2x+x=36+36,
∴x=24.
②当AD=DE时,
∵36+36+2x+x=180,
∴x=36.
③当EA=DE时,
∵90- x+36+36+x=180,
∴x不存在,应舍去.
综合上述:满足条件的x=24或 36.



科目:初中数学 来源: 题型:
【题目】某地连续九天的最高气温统计如下表:
最高气温(℃) | 22 | 23 | 24 | 25 |
天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A. 24,25 B. 24.5,25 C. 25,24 D. 23.5,24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,如图,使点A和点B重合,折痕与AB、AC分别相交于点D和点E,折痕DE的长为
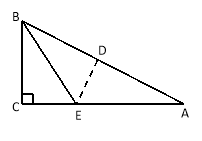
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.
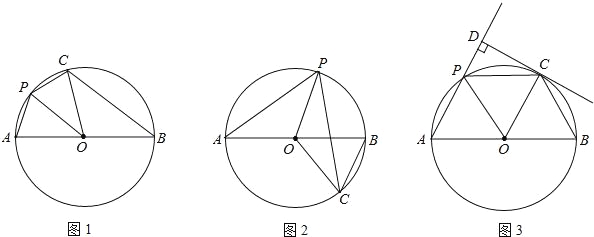
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
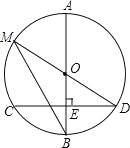
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com