
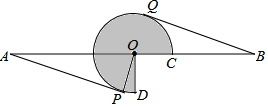
 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.
如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.分析 (1)连接OQ.只要证明Rt△APO≌Rt△BQO即可解决问题;
(2)求出优弧DQ的圆心角以及半径即可解决问题;
(3)由△APO的外心是OA的中点,OA=8,推出△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8;
解答 (1)证明:连接OQ.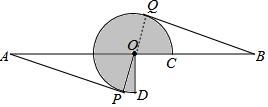
∵AP、BQ是⊙O的切线,
∴OP⊥AP,OQ⊥BQ,
∴∠APO=∠BQO=90°,
在Rt△APO和Rt△BQO中,
$\left\{\begin{array}{l}{OA=OB}\\{OP=OQ}\end{array}\right.$,
∴Rt△APO≌Rt△BQO,
∴AP=BQ.
(2)∵Rt△APO≌Rt△BQO,
∴∠AOP=∠BOQ,
∴P、O、Q三点共线,
∵在Rt△BOQ中,cosB=$\frac{QB}{OB}$=$\frac{4\sqrt{3}}{8}$=$\frac{\sqrt{3}}{2}$,
∴∠B=30°,∠BOQ=60°,
∴OQ=$\frac{1}{2}$OB=4,
∵∠COD=90°,
∴∠QOD=90°+60°=150°,
∴优弧$\widehat{QD}$的长=$\frac{210•π•4}{180}$=$\frac{14}{3}$π,
(3)∵△APO的外心是OA的中点,OA=8,
∴△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8.
点评 本题考查切线的性质、弧长公式、全等三角形的判定和性质、三角形的外心等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
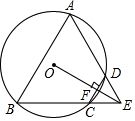 如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,若AB=BE.
如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,若AB=BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
| 销量(斤) | 80-3x | 120-x | |
| 储存和损耗费用(元) | 40+3x | 3x2-64x+400 | |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩/分 | 66 | 67 | 68 | 69 | 70 |
| 人数 | 1 | 4 | 1 | 2 | 2 |
| A. | 67,67.5 | B. | 68,68 | C. | 68,67.5 | D. | 67.5,68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com