
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线p=ax2-10ax+8(a>0)经过点C、D,则点B的坐标为________.

【答案】(4,0)
【解析】
根据抛物线p=ax210ax+8(a>0)经过点C、D和二次函数图象具有对称性,可以求得该抛物线顶点的横坐标和CD的长,然后根据菱形的性质和勾股定理可以求得AO的长,从而可以求得OB的长,进而写出点B的坐标.
解:∵抛物线p=ax210ax+8=a(x5)225a+8,
∴该抛物线的顶点的横坐标是x=5,当x=0时,y=8,
∴点D的坐标为:(0,8),
∴OD=8,
∵抛物线p=ax210ax+8(a>0)经过点C、D,CD∥AB∥x轴,
∴CD=5×2=10,
∴AD=10,
∵∠AOD=90°,OD=8,AD=10,
∴AO=![]() ,
,
∵AB=10,
∴OB=10AO=106=4,
∴点B的坐标为(4,0),
故答案为:(4,0)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
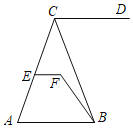
【题目】如图,EF∥AB,∠DCB=65°,∠CBF=15°,∠EFB=130°.
(1)直线CD与AB平行吗?为什么?
(2)若∠CEF=68°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
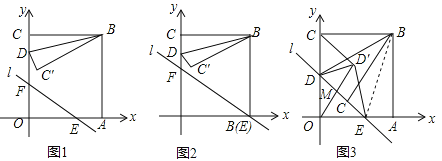
【题目】(2016浙江省衢州市)如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育。若购进甲种2株,乙种3株,则共需成本l700元;若购进甲种3株,乙种l株.则共需成本l500元。
(1)求甲、乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购入甲、乙两种君子兰,若购入乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数![]() 的点称为基准点,记作点
的点称为基准点,记作点![]() .对于两个不同的点
.对于两个不同的点![]() 和
和![]() ,若点
,若点![]() 、点
、点![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 和点
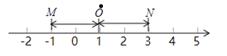
和点![]() 互为基准变换点.例如:下图中,点
互为基准变换点.例如:下图中,点![]() 表示数
表示数![]() ,点N表示数
,点N表示数![]() ,它们与基准点
,它们与基准点![]() 的距离都是
的距离都是![]() 个单位长度,点
个单位长度,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
(1)已知点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
①若![]() ,则
,则![]() _______ ;
_______ ;
②用含![]() 的式子表示
的式子表示![]() ,则
,则![]() _____;
_____;
(2)对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动
,再把所得数表示的点沿着数轴向左移动![]() 个单位长度得到点
个单位长度得到点![]() .若点
.若点![]() 与点
与点![]() 互为基准变换点,则点
互为基准变换点,则点![]() 表示的数是_____________;
表示的数是_____________;
(3)点![]() 在点
在点![]() 的左边,点
的左边,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.对
个单位长度.对![]() 、
、![]() 两点做如下操作:点
两点做如下操作:点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论
.若无论![]() 为何值,
为何值,![]() 与
与![]() 两点间的距离都是
两点间的距离都是![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数 1 至 2024 按一定规律排列成如图所示的 8 列,规定从上到下依次为第 1 行,第 2 行,第 3 行,…从左往右依次为第 1 列至第 8 列.
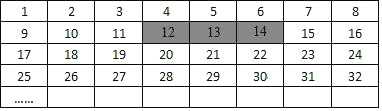
(1)数 56 在第 行 列 ;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为 x,则被框的三个数的和能否等于 2019?若能,请求出 x;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com