解:(1)直角三角形,
证明:∵平行四边形ABCD,
∴AD∥BC,
∴∠DAB+∠ABC=180°,
∵AP与BP分别平分∠DAB和∠CBA,
∴∠PAB=

∠DAB,∠PBA=

∠CBA,
∴∠PAB+∠PBA=90°,
∴∠APB=180°-90°=90°,
∴△APB是直角三角形.

(2)相等,
理由是:∵平行四边形ABCD,
∴DC∥AB,AD=BC,
∴∠DPA=∠PAB,∠CPB=∠PBA,
∵AP与BP分别平分∠DAB和∠CBA,
∴∠PAB=∠DAP,∠PBC=∠PBA,
∴∠DPA=∠DAP,∠CPB=∠CBP,
∴DP=AD,CP=BC,
∴DP=CP.
(3)∵AB是圆Q的直径,
∴∠AEB=∠APB=90°,
∵AP平分∠DAB,
∴∠DAP=∠BAP,
∴△AEF∽△APB,
∴∠AFE=∠APB,
∵平行四边形ABCD,
∴DC∥AB,
∴∠ABP=∠BPC,
∵AD=50,
∴AB=2AD=100,
在△APB中,由勾股定理得:PB=60,
∴tan∠AFE=tan∠APB=
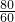
=

.
(4)∵AP=80,AB=2AD=100,

在△APB中,由勾股定理得:BP=60,
过P作PH⊥AB于H,
由三角形的面积公式得:AP×BP=AB×PH,
∴PH=48,
由平行四边形的面积公式得:AD×BE=AB×PH,
BE=96,
在△ABE中,由勾股定理得:AE=

=28,
∵tan∠AFE=

,
∴tan∠EAF=tan∠FAB=

,
∴

=

,
∵O′M=m,
∴AO′=

m,
BO′=100-

m,
过O′作O′N⊥BF于N,
则O′N=m,
∵O′N∥AE,
∴

=

,
∴
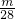
=

,
解得:m=
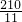
,
答:m为
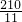
时,⊙O′与AP、BF都相切.
分析:(1)根据平行四边形性质推出∠DAB+∠ABC=180°,根据角平分线定义求出∠PAB+∠PBA=90°,根据三角形的内角和定理求出即可;
(2)根据平行线的性质推出∠DA=∠PAB,推出∠DPA=∠DAP即可;
(3)证△AEF∽△APB,推出∠AFE=∠APB,证∠ABP=∠BPC,根据勾股定理求出BP,即可求出答案;
(4)过P作PH⊥AB于H,过O′作O′N⊥BF于N,求出高PH长,根据平行四边形面积求出BE,根据勾股定理求出AE,求出AO′=

m,根据O′N∥AE,得出比例式

=

,代入求出即可.
点评:本题综合考查了对平行四边形的性质,锐角三角函数,三角形的面积,勾股定理,切线的性质和判定,角平分线定义,三角形的内角和定理等知识点的应用,此题综合性比较强,有一定的难度,对学生提出较高的要求,综合运用这些性质进行推理和计算是解此题的关键.

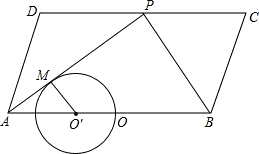 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm. ∠DAB,∠PBA=
∠DAB,∠PBA= ∠CBA,
∠CBA, (2)相等,
(2)相等,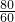 =
= .
.
 =28,
=28, ,
, ,
, =
= ,
, m,
m, m,
m, =
= ,
,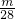 =
= ,
,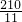 ,
,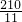 时,⊙O′与AP、BF都相切.
时,⊙O′与AP、BF都相切. m,根据O′N∥AE,得出比例式
m,根据O′N∥AE,得出比例式 =
= ,代入求出即可.
,代入求出即可.

 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2