
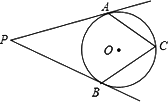
如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果∠ACB=70°,那么∠P的度数是________.
|
分析:连接OA,OB,由PA与PB都为圆O的切线,利用切线的性质得到OA垂直于AP,OB垂直于BP,可得出两个角为直角,再由同弧所对的圆心角等于所对圆周角的2倍,由已知∠ACB的度数求出∠AOB的度数,在四边形PABO中,根据四边形的内角和定理即可求出∠P的度数. 解答:解:连接OA,OB,如图所示:
∵PA、PB是⊙O的切线, ∴OA⊥AP,OB⊥BP, ∴∠OAP=∠OBP=90°, 又∵圆心角∠AOB与圆周角∠ACB都对 ∴∠AOB=2∠ACB=140°, 则∠P=360°-(90°+90°+140°)=40°. 点评:此题考查了切线的性质,四边形的内角与外角,以及圆周角定理,连接OA与OB,熟练运用性质及定理是解本题的关键. |
|
切线的性质;多边形内角与外角;圆周角定理 |


科目:初中数学 来源: 题型:
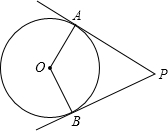 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com