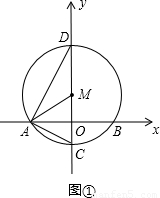
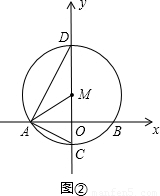
是否存在一个三角形的三边长恰是三个连续正整数,且其中一个内角等于另一内角2倍的△ABC?证明你的结论.
解:

存在满足条件的三角形
当△ABC 的三边长分别为 a=6,b=4,c=5时,∠A=2∠B
如图,当∠A=2∠B时,延长BA至点D,使AD=AC=b,连接CD,则△ACD为等腰三角形
∵∠BAC为△ACD的一个外角,∴∠BAC=2∠D
由已知∠BAC=2∠B,则∠B=∠D
∴△CBD为等腰三角形
又∠D为△ACD与△CBD 的一个公共角,∴△ACD∽△CBD
于是

=
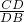
,即

=
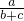
,
∴a
2=b(b+c)
∵6
2=4(4+5),∴此三角形满足题设条件
故存在满足条件的三角形
说明:满足条件的三角形不是唯一的,
若∠A=2∠B,得a
2=b(b+c),有以下三种情形:
(1)当a>c>b时,设a=n+1,c=n,b=n-1(n为大于1的正整数)
代入a
2=b(b+c),得(n+1)
2=(n-1)(2n-1)
解得n=5
∴a=6,b=4,c=5
(2)当c>a>b时,设c=n+1,a=n,b=n-1(n为大于1的正整数)
代入a
2=b(b+c),得n
2=2n(n-1)
解得n=2
∴a=2,b=1,c=3,此时不能构成三角形
(3)当a>b>c时,设a=n+1,b=n,c=n-1(n为大于1的正整数)
代入a
2=b(b+c),得(n+1)
2=n(2n-1)
即n
2-3n-1=0,此方程无整数解
所以,三边长恰为三个连续的整数,且其中一个内角等于另一个内角2倍的三角形存在,而且只有三边长分别为4、5、6构成的三角形满足条件
分析:如图,当∠A=2∠B时,延长BA至点D,使AD=AC=b,连接CD,则△ACD为等腰三角形,若∠A=2∠B,得a
2=b(b+c),有以下三种情形:
(1)当a>c>b时,(2)当c>a>b时,(3)当a>b>c时分别得出即可.
点评:本题是一道综合题,考查了三角形的内切圆和三角形的面积,难度较大.

 存在满足条件的三角形
存在满足条件的三角形 =
=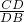 ,即
,即 =
=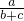 ,
,

 名校课堂系列答案
名校课堂系列答案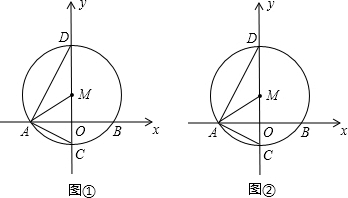
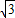 )为圆心,以2
)为圆心,以2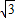 为半径作⊙M交x轴于A、B两点,交y轴的负半轴于点C,连接AM、AC、AD.
为半径作⊙M交x轴于A、B两点,交y轴的负半轴于点C,连接AM、AC、AD.