
分析 (1)根据分式的除法法则计算;
(2)根据分式的基本性质解答.
解答 解:(1)计算:$\frac{4ac}{3b}÷\frac{{9{b^3}}}{{2a{c^2}}}$=$\frac{4ac}{3b}$×$\frac{2a{c}^{2}}{9{b}^{3}}$=$\frac{8{a}^{2}{c}^{3}}{27{b}^{4}}$;
(2)系数化成整数:$\frac{0.25a-0.2b}{0.1a+0.3b}$=$\frac{5a-4b}{2a+6b}$.
故答案为:(1)$\frac{8{a}^{2}{c}^{3}}{27{b}^{4}}$;(2)$\frac{5a-4b}{2a+6b}$.
点评 本题考查的是分式的乘除法、分式的化简,掌握分式的乘方法法则、分式的基本性质是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
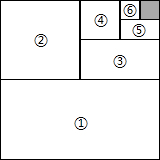 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
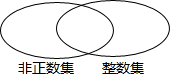 如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?
如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com