练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

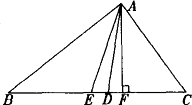
    　　如图①AD是△ABC的角平分线，

    　　则∠________＝∠________＝∠________；

    　　②AE是△ABC的中线，

    　　则________＝________＝________；

    　　③AF是△ABC的高，则∠________＝∠________＝90°．

    答案：
    解析：

    　　①BAD　CAD　BAC

    　　②BE　CE　BC

    　　③AFB　AFC


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学教研室 题型：044

    　　如图，在ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F。四边形AFCE是菱形吗？请说明理由。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    阅读以下内容：

    　　如图(1)，在ABC中，由DE∥BC，我们可以得到△ADE∽△ABC，

    从而有　　，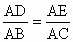

    即AD·AC=AE·AB，于是

    AD·(AE+EC)=AE·(AD+DB)，

    AD·EC=AE·DB，

    从而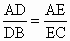，即△ABC中BC的平行线DE将另两条边AB、AC分割为成比例的线段．

    我们已经知道，如果D是AB的中点，则E是AC的中点．

    现在请你回答下列问题，并说说你的理由：

    (1)如图(2)，DE∥FG∥BC，AD=DF=FB，那么AE、EG、GC有什么关系？

    (2)如图(3)，DE∥FG∥BC，DF=FB，那么EG与GC有什么关系？

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年湖北省鄂州市第三中学八年级下学期期中考试数学试卷（带解析） 题型：解答题

    [问题情境] 勾股定理是一条古老的数学定理，它有很多证明方法，我国汉代数学家赵爽根据弦图利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。
    [定理表述] 请你根据图（1）中的直角三角形叙述勾股定理（用文字及符号语言叙述）；
    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
     
    [尝试证明]　以图（1）中的直角三角形为基础可以构造出以a、b为底，以a＋b为高的直角梯形如图（2）。请你利用图（2）验证勾股定理；
    [知识拓展]　利用图(2)的直角梯形，我们可以证明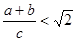，其证明步骤如下：
    ∵BC＝a＋b，AD＝    　    .
    又∵在直角梯形ABCD中有直角腰BC　　　　斜腰AD（填“＞”，“＜”或“＝”），即　　　　　　　。
    ∴

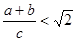
    查看答案和解析>>

    科目：初中数学 来源：2014届湖北省鄂州市八年级下学期期中考试数学试卷（解析版） 题型：解答题

    [问题情境] 勾股定理是一条古老的数学定理，它有很多证明方法，我国汉代数学家赵爽根据弦图利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。

    [定理表述] 请你根据图（1）中的直角三角形叙述勾股定理（用文字及符号语言叙述）；

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

     

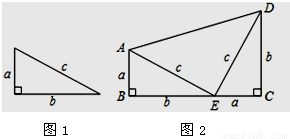
    [尝试证明]　以图（1）中的直角三角形为基础可以构造出以a、b为底，以a＋b为高的直角梯形如图（2）。请你利用图（2）验证勾股定理；

    [知识拓展]　利用图(2)的直角梯形，我们可以证明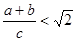，其证明步骤如下：

    ∵BC＝a＋b，AD＝    　    .

    又∵在直角梯形ABCD中有直角腰BC　　　　斜腰AD（填“＞”，“＜”或“＝”），即　　　　　　　。

    ∴

     

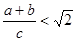
    查看答案和解析>>

    同步练习册答案