练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．关于x的不等式4x-a＜0的正整数只有1，2，求a的取值范围．

    分析 先求出不等式的解集，再根据其正整数解列出不等式，解此不等式即可．

    解答 解：解不等式得：x＜$\frac{a}{4}$，
    ∵正整数解为1，2，
    ∴2＜$\frac{a}{4}$≤3，
    解得：8＜a≤12．

    点评 本题考查了一元一次不等式的整数解，根据x的取值范围，确定$\frac{a}{4}$的范围是解题的关键．再解不等式时要根据不等式的基本性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．如图是每个面都标注了字母的立方体的表面展开图．在展开前，与标注字母c的面相对的面上的字母为（　　）
    A．aB．dC．eD．f

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知菱形ABCD中，对角线AC与BD相交于点O，∠BAD=120°，AC=4，则该菱形的面积是（　　）
    A．16$\sqrt{3}$B．8$\sqrt{3}$C．4$\sqrt{3}$D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列事件中，是确定事件的有（　　）
    A．打开电视，正在播放广告B．三角形三个内角的和是180°
    C．两个负数的和是正数D．某名牌产品一定是合格产品

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，E、F、G、H分别是菱形ABCD四边的中点，菱形ABCD的面积为4$\sqrt{3}$cm2，对角线AC=2$\sqrt{2}$cm．
    （1）求菱形ABCD对角线BD的长；
    （2）求四边形EFGH的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，已知等边△ABC的边长是2cm，将边AC沿射线BC的方向平移2cm，得到线段DE，连接AD、CE．
    （1）求证：四边形ACED是菱形；
    （2）将△ABC绕点C旋转，当CA′与DE交于一点M，CB′与AD交于一点N时，点M、N和点D构成△DMN，试探究△DMN的周长是否存在最小值？如果存在，求出该最小值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．将抛物线C1：y=-x2-2x，绕着点M（1，0）旋转180°后，所得到的新抛物线C2的解析式是y=（x-3）2-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

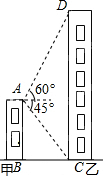    3．如图，甲楼AB的高度为100米，自甲楼楼顶A处，测得乙楼顶端D处的仰角为60°，测得乙楼底部C处的俯角为45°，求乙楼CD的高度（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．化简求值：$\frac{a-b}{\sqrt{a}-\sqrt{b}}$-$\frac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}$，其中a=17，b=4．

    查看答案和解析>>

    同步练习册答案