
| 1 |
| 2 |
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD-∠BOC=2α,∴∠AOD=
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14° |

 解:(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,
解:(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
 (2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,| 1 |
| 2 |
 ∴∠BOC=10°;
∴∠BOC=10°;| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |


科目:初中数学 来源: 题型:
 三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?
三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
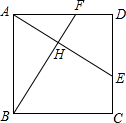 如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H
如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H查看答案和解析>>
科目:初中数学 来源: 题型:
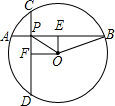 如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,
如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com