
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx©3a£Øa”Ł0£©ÓėxÖį½»ÓŚµćA£Ø©1£¬0£©ŗĶµćB£¬ÓėyÖį½»ÓŚµćC£Ø0£¬2£©£¬Į¬½ÓBC£®
£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½ŗĶ¶Ō³ĘÖį£¬²¢Š“³öĻ߶ĪBCµÄÖŠµć×ų±ź£»
£Ø2£©½«Ļ߶ĪBCĻČĻņ×óĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬ŌŁĻņĻĀĘ½ŅĘmøöµ„Ī»³¤¶Č£¬Ź¹µćCµÄ¶ŌÓ¦µćC1Ē”ŗĆĀäŌŚøĆÅ×ĪļĻßÉĻ£¬Ēó“ĖŹ±µćC1µÄ×ų±źŗĶmµÄÖµ£»
£Ø3£©ČōµćPŹĒøĆÅ×ĪļĻßÉĻµÄ¶Æµć£¬µćQŹĒøĆÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄ¶Æµć£¬µ±ŅŌP£¬Q£¬B£¬CĖĵćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬Ēó“ĖŹ±µćPµÄ×ų±ź£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗ”ßÅ×ĪļĻßy=ax2+bx©3a£Øa”Ł0£©ÓėxÖį½»ÓŚµćA£Ø©1£¬0£©ŗĶµćB£¬ÓėyÖį½»ÓŚµćC£Ø0£¬2£©£¬
”ą ![]() £¬
£¬
½āµĆ  £®
£®
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=© ![]() x2+
x2+ ![]() x+2=©
x+2=© ![]() £Øx©1£©2+2
£Øx©1£©2+2 ![]() £¬
£¬
”ą¶Ō³ĘÖįŹĒx=1£¬
”ß1+£Ø1+1£©=3£¬
”ąBµć×ų±źĪŖ£Ø3£¬0£©£¬
”ąBCµÄÖŠµć×ų±źĪŖ£Ø1.5£¬1£©
£Ø2£©
½ā£ŗ”ßĻ߶ĪBCĻČĻņ×óĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬ŌŁĻņĻĀĘ½ŅĘmøöµ„Ī»³¤¶Č£¬Ź¹µćCµÄ¶ŌÓ¦µćC1Ē”ŗĆĀäŌŚøĆÅ×ĪļĻßÉĻ£¬
”ąµćC1µÄŗį×ų±źĪŖ©2£¬
µ±x=©2Ź±£¬y=© ![]() ”Į£Ø©2£©2+
”Į£Ø©2£©2+ ![]() ”Į£Ø©2£©+2=©
”Į£Ø©2£©+2=© ![]() £¬
£¬
”ąµćC1µÄ×ų±źĪŖ£Ø©2£¬© ![]() £©£¬
£©£¬
m=2©£Ø© ![]() £©=5
£©=5 ![]()
£Ø3£©
½ā£ŗ¢ŁČōBCĪŖĘ½ŠŠĖıߊĪµÄŅ»±ß£¬
”ßBCµÄŗį×ų±źµÄ²īĪŖ3£¬
”ßµćQµÄŗį×ų±źĪŖ1£¬
”ąPµÄŗį×ų±źĪŖ4»ņ©2£¬
”ßPŌŚÅ×ĪļĻßÉĻ£¬
”ąPµÄׯ×ų±źĪŖ©3 ![]() £¬
£¬
”ąP1£Ø4£¬©3 ![]() £©£¬P2£Ø©2£¬©3
£©£¬P2£Ø©2£¬©3 ![]() £©£»
£©£»
¢ŚČōBCĪŖĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻߣ¬
ŌņBCÓėPQ»„ĻąĘ½·Ö£¬
”ßµćQµÄŗį×ų±źĪŖ1£¬BCµÄÖŠµć×ų±źĪŖ£Ø1.5£¬1£©£¬
”ąPµćµÄŗį×ų±źĪŖ1.5+£Ø1.5©1£©=2£¬
”ąPµÄׯ×ų±źĪŖ© ![]() ”Į22+
”Į22+ ![]() ”Į2+2=2£¬
”Į2+2=2£¬
”ąP3£Ø2£¬2£©£®
×ŪÉĻĖłŹö£¬µćPµÄ×ų±źĪŖ£ŗP1£Ø4£¬©3 ![]() £©£¬P2£Ø©2£¬©3
£©£¬P2£Ø©2£¬©3 ![]() £©£¬P3£Ø2£¬2£©
£©£¬P3£Ø2£¬2£©
”¾½āĪö”æ£Ø1£©°ŃµćA£Ø©1£¬0£©ŗĶµćC£Ø0£¬2£©µÄ×ų±ź“śČėĖłøųÅ×ĪļĻßæɵĆa”¢bµÄÖµ£¬½ų¶ųµĆµ½øĆÅ×ĪļĻߵĽāĪöŹ½ŗĶ¶Ō³ĘÖį£¬ŌŁĒó³öµćBµÄ×ų±ź£¬øł¾ŻÖŠµć×ų±ź¹«Ź½Ēó³öĻ߶ĪBCµÄÖŠµć×ų±ź¼“æÉ£»£Ø2£©øł¾ŻĘ½ŅʵĊŌÖŹæÉÖŖ£¬µćCµÄ¶ŌÓ¦µćC1µÄŗį×ų±źĪŖ©2£¬ŌŁ“śČėÅ×ĪļĻßæÉĒóµćC1µÄ×ų±ź£¬½ųŅ»²½µĆµ½mµÄÖµ£»£Ø3£©B”¢CĪŖ¶Øµć£¬æÉ·ÖBCĪŖĘ½ŠŠĖıߊĪµÄŅ»±ß¼°¶Ō½ĒĻßĮ½ÖÖĒéæöĢ½ĢֵƵ½µćPµÄ×ų±ź£®
”¾æ¼µć¾«Īö”æ½ā“š“ĖĢāµÄ¹Ų¼üŌŚÓŚĄķ½ā¶ž“ĪŗÆŹżµÄŠŌÖŹµÄĻą¹ŲÖŖŹ¶£¬ÕĘĪÕŌö¼õŠŌ£ŗµ±a>0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ų¼õŠ”£»¶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ųŌö“ó£»µ±a<0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ųŌö“󣻶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ų¼õŠ”£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
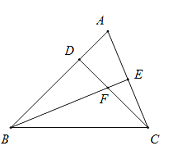
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬BA=BC£¬BEĘ½·Ö”ĻABC£¬CD”ĶBD£¬ĒŅCD=BD£®
£Ø1£©ĒóÖ¤£ŗBF=AC£»
£Ø2£©ČōAD=![]() £¬ĒóCFµÄ³¤£®
£¬ĒóCFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
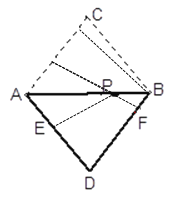
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AC=BC=5£¬AB=6,½«ĖüŃŲAB·ÕŪµĆµ½”÷ABD£¬µćP”¢E”¢F·Ö±šĪŖĻ߶ĪAB”¢AD”¢DBµÄČĪŅāµć£¬ŌņPE+PFµÄ×īŠ”ÖµŹĒ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖćĻĀĮŠø÷Ģā
£Ø1£©¼ĘĖć£ŗ ![]() ©£Ø
©£Ø ![]() £©©1+£Ø¦Š©
£©©1+£Ø¦Š© ![]() £©0©£Ø©1£©100£»
£©0©£Ø©1£©100£»
£Ø2£©ŅŃÖŖ|a+1|+£Øb©3£©2=0£¬Ē󓜏żŹ½£Ø ![]() ©
© ![]() £©”Ā
£©”Ā ![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬µćEŹĒ¶Ō½ĒĻßACÉĻŅ»µć£¬ĒŅCE=CD£¬¹żµćE×÷EF”ĶAC½»ADÓŚµćF£¬Į¬½ÓBE£® 
£Ø1£©ĒóÖ¤£ŗDF=AE£»
£Ø2£©µ±AB=2Ź±£¬ĒóBE2µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=BC£¬µćDŌŚABµÄŃÓ³¤ĻßÉĻ£® 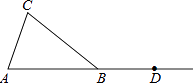
£Ø1£©ĄūÓĆ³ß¹ę°“ĻĀĮŠŅŖĒó×÷Ķ¼£¬²¢ŌŚĶ¼ÖŠ±źĆ÷ĻąÓ¦µÄ×ÖÄø£Ø±£Įō×÷Ķ¼ŗŪ¼££¬²»Š“×÷·Ø£©£® ¢Ł×÷”ĻCBDµÄĘ½·ÖĻßBM£»
¢Ś×÷±ßBCÉĻµÄÖŠĻßAE£¬²¢ŃÓ³¤AE½»BMÓŚµćF£®
£Ø2£©ÓÉ£Ø1£©µĆ£ŗBFÓė±ßACµÄĪ»ÖĆ¹ŲĻµŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻABC£½90”ć£¬AB£½BC£¬Ö±Ļßl1”¢l2”¢l3·Ö±šĶعżA”¢B”¢CČżµć£¬ĒŅl1”Īl2”Īl3£®Čōl1Óėl2µÄ¾ąĄėĪŖ4£¬l2Óėl3µÄ¾ąĄėĪŖ6£¬ŌņRt”÷ABCµÄĆ껿ĪŖ___________£®
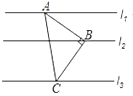
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½Ķ¬Ń§µÄ¼ŅÓėѧŠ£µÄ¾ąĄė¾łĪŖ3000Ć×£®¼×Ķ¬Ń§ĻČ²½ŠŠ600Ć×£¬Č»ŗó³Ė¹«½»³µČ„ѧŠ££¬ŅŅĶ¬Ń§Ęļ×ŌŠŠ³µČ„ѧŠ££®ŅŃÖŖ¼×²½ŠŠĖŁ¶ČŹĒŅŅĘļ×ŌŠŠ³µĖŁ¶ČµÄ![]() £¬¹«½»³µµÄĖŁ¶ČŹĒŅŅĘļ×ŌŠŠ³µĖŁ¶ČµÄ2±¶£®¼×ŅŅĮ½Ķ¬Ń§Ķ¬Ź±“Ó¼Ņ³ö·¢Č„ѧŠ££¬½į¹ū¼×Ķ¬Ń§±ČŅŅĶ¬Ń§Ōēµ½2·ÖÖÓ£®ŅŅĘļ×ŌŠŠ³µµÄĖŁ¶ČŹĒ£Ø””””£©Ć×/·Ö£®
£¬¹«½»³µµÄĖŁ¶ČŹĒŅŅĘļ×ŌŠŠ³µĖŁ¶ČµÄ2±¶£®¼×ŅŅĮ½Ķ¬Ń§Ķ¬Ź±“Ó¼Ņ³ö·¢Č„ѧŠ££¬½į¹ū¼×Ķ¬Ń§±ČŅŅĶ¬Ń§Ōēµ½2·ÖÖÓ£®ŅŅĘļ×ŌŠŠ³µµÄĖŁ¶ČŹĒ£Ø””””£©Ć×/·Ö£®
A. 600 B. 400 C. 300 D. 150
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬D ŹĒ AB ±ßÉĻµÄÖŠµć£¬½«”÷ABC ŃŲ¹żµć D µÄÖ±ĻßÕŪµž£¬DE ĪŖÕŪŗŪ£¬Ź¹µć A ĀäŌŚ BC ÉĻ F“¦£¬Čō”ĻB=40”ć£¬Ōņ”ĻEDF=_____¶Č.

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com