练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     直角坐标系中，已知点A（4，0），点P在第一象限内的直线y＝－x＋6上，设△OPA的面积为S。

        ①S与y具有怎样的函数关系？求出自变量y的取值范围

    ②S与x具有怎样的函数关系？求出自变量x的取值范围

        ③当S＝10时。求点P的坐标。

    解：△OAP中，边OA长为定值，则S为PB长的函数，但PB长即为点P的纵坐标,则可得到S与y的函数关系式；

    又点P在直线y＝－x＋6上， ∴可得S关于x的函数关系式

    ①∵

    ∴                          

    ②∵点P（x，y）在直线y＝－x＋6上，

    ∴(0≦X<6)

    ①当S＝10时，2y＝10，∴y＝5

    当y＝5时，5＝－x＋6 ∴ x＝1    ∴P(1，5)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

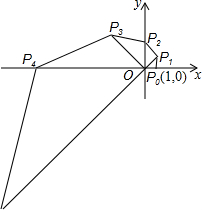    精英家教网如图，在直角坐标系中，已知点P0的坐标为（1，0），将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OPn（n为正整数）．我们规定：把点Pn（xn，yn）（n=0，1，2，3，…）的横坐标xn、纵坐标yn都取绝对值后得到的新坐标（|xn|，|yn|）称之为点Pn的“绝对坐标”．则Pn的“绝对坐标”为（　　）
    A、（2n-1
    		2
    ，2n-1
    		2
    ）或（2n，0）
    B、（2n，0）或（0，2n）
    C、（0，2n）或（2n-1
    		2
    ，2n-1
    		2
    ）
    D、（2n-1
    		2
    ，2n-1
    		2
    ）或（2n，0）或（0，2n）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在直角坐标系中，已知点A（-3，2），B（2，-4），在x轴上找一点C，使AC+BC最短，则点C的坐标为（　　）
    A、(0，-
    5
    8
    )
    B、(-
    4
    3
    ，0)
    C、（-4，0）
    D、(
    4
    3
    ，0)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

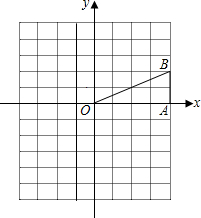    如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．
    （1）画出将△OAB绕原点逆时针旋转90°后所得的△OA1B1；
    （2）并写出点A1、B1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系中，已知点A（-3，4）和点B，若△AOB是等腰直角三角形，∠AOB=90°，则点B的坐标是
    （4，3）或（-4，-3）
    （4，3）或（-4，-3）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在直角坐标系中，已知点B（-3，3），点A（1，1），在x轴和y轴上确定点P，使△ABP为等腰三角形，则符合条件的点P的个数共有（　　）

    查看答案和解析>>

    同步练习册答案