
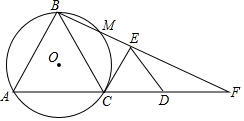
 如图,C为线段AD上一点,△ABC和△CDE都是等边三角形,连接BE并延长,交AD长线于F,△ABC的外接圆⊙O交BF于点M.
如图,C为线段AD上一点,△ABC和△CDE都是等边三角形,连接BE并延长,交AD长线于F,△ABC的外接圆⊙O交BF于点M.分析 (1)连结OC、OA,如图,利用圆周角定理得到∠AOC=2∠B=120°,再根据等腰三角形的性质和三角形内角和可计算出∠OCA=30°,再加上∠ECD=60°,所以∠OCE=90°,然后根据切线的判定方法可判断CE为⊙O的切线;
(2)连接AM,如图,先证明△BAM∽△BFA,然后利用相似比即可得到结论;
(3)由于$\frac{{S}_{3}}{{S}_{1}}$=$\frac{1}{4}$,△DGH∽△ABC,则根据相似三角形的性质得$\frac{GH}{BC}$=$\frac{1}{2}$,则由GH∥BC得到$\frac{FH}{FC}$=$\frac{GH}{BC}$=$\frac{1}{2}$,所以CF=2FH,再利用GH∥ED,DG∥CE得到$\frac{GH}{DE}$=$\frac{FH}{FD}$,$\frac{DG}{CE}$=$\frac{FD}{CF}$,利用等量代换可得到FD2=FH•FD,所以FD2=2FH2,即FD=$\sqrt{2}$FH,接着由DE∥BC得到$\frac{DE}{BC}$=$\frac{FD}{FC}$=$\frac{\sqrt{2}}{2}$,然后利用△CDE∽△ABC,根据相似三角形的性质可求出S2的值.
解答 (1)证明:连结OC、OA,如图,
∵⊙O为等边△ABC的外心,
∴∠AOC=2∠B=2×60°=120°,
而OA=OC,
∴∠OCA=$\frac{1}{2}$(180°-120°)=30°,
∵△CDE为等边三角形,
∴∠ECD=60°,
∴∠OCE=180°-30°-60°=90°,
∴OC⊥CE,
∴CE为⊙O的切线;
(2)证明:连接AM,如图,
∵∠AMB=∠ACB=60°,
而∠BAC=60°,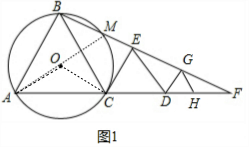
∴∠AMB=∠BAF,
而∠ABM=∠FBA,
∴△BAM∽△BFA,
∴AB:BF=BM:AB,
∴AB2=BM•BF;
(3)解:∵$\frac{{S}_{3}}{{S}_{1}}$=$\frac{2}{8}$=$\frac{1}{4}$,
而△DGH∽△ABC,
∴$\frac{GH}{BC}$=$\frac{1}{2}$,
∵GH∥BC,
∴$\frac{FH}{FC}$=$\frac{GH}{BC}$=$\frac{1}{2}$,
∴CF=2FH,
∵GH∥ED,DG∥CE,
∴$\frac{GH}{DE}$=$\frac{FH}{FD}$,$\frac{DG}{CE}$=$\frac{FD}{CF}$,
而GH=DG,DE=CE,
∴$\frac{FH}{FD}$=$\frac{FD}{CF}$,即FD2=FH•FD,
而CF=2FH,
∴FD2=2FH2,
∴FD=$\sqrt{2}$FH,
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{FD}{FC}$=$\frac{FD}{2FH}$=$\frac{\sqrt{2}FH}{2FH}$=$\frac{\sqrt{2}}{2}$,
∵△CDE∽△ABC,
∴$\frac{{S}_{2}}{{S}_{3}}$=($\frac{\sqrt{2}}{2}$)2=$\frac{1}{2}$,
∴S2=$\frac{1}{2}$×8=4.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、切线的判定和等边三角形的性质;能灵活应用平行线分线段成比例、相似三角形的判定与性质表示线段之间的关系.特别第(3)问中平行线比较多,合理选择比例线段很关键.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
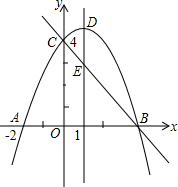 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
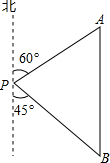 五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果保留根号)
五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com