
【题目】如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.

【答案】(1)61°;(2)30°.
【解析】
(1)求出∠AOD和∠BOD,由OC平分∠DOB,求出∠BOC;
(2)根据OC平分∠BOD,OD平分∠AOC得出∠BOC=∠DOC=∠AOD,求出∠AOD即可得出∠AOE.
解:(1)∠AOD=∠DOE﹣∠AOE=90°﹣32°=58°,,
∠BOD=∠AOB﹣∠AOD=180°﹣58°=122°,
又OC平分∠BOD,
所以:∠BOC=![]() ∠BOD=
∠BOD=![]() ×122°=61°;
×122°=61°;
(2)因为OC平分∠BOD,OD平分∠AOC,
所以∠BOC=∠DOC=∠AOD,
又∠BOC+∠DOC+∠AOD=180°,
所以∠AOD=![]() ×180°=60°,
×180°=60°,
所以∠AOE=∠DOE﹣∠AOD=90°﹣60°=30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( ) 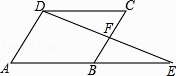
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2= ![]() (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )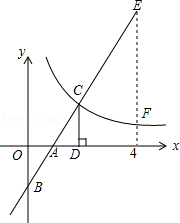
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平移线段AB,使点A移动到点A1.
(1)画出平移后的线段A1B1,分别连接AA1,BB1.
(2)分别画出AC⊥A1B1于点C,AD⊥BB1于点D.
(3)AA1与BB1之间的距离,就是线段 的长度.
(4)线段AB平移的距离,就是线段 的长度.
(5)线段BD的长度,是点B到直线 的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块长为a米,宽为b米的矩形空地建成一个矩形花园,要求在花园中修两条入口宽均为x米的小道,其中一条小道两边分别经过矩形一组对角顶点,剩余的地方种植花草,现有从左至右三种设计方案如图所示,种植花草的面积分别为S1,S2和S3,则它们的大小关系为( )

A. S3<S1<S2 B. S1<S2<S3 C. S2<S1<S3 D. S1=S2=S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y= ![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )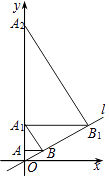
A.(0,42015)
B.(0,42014)
C.(0,32015)
D.(0,32014)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. 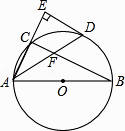
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com