
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����y=-x��ͼ��l�ǵڶ��������Ľ�ƽ���ߣ�
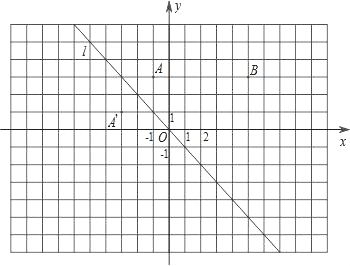
��1��ʵ����̽������ͼ�۲���֪A��-1��3������ֱ��l�ĶԳƵ�A�������Ϊ��-3��1��������д����B��5��3������ֱ��l�ĶԳƵ�B�������Ϊ ��
��2�������뷢�֣����ͼ�Σ��Լ�ѡ������һ�ԣ�ͨ���۲������꣬��ᷢ�֣�����ƽ������һ��P��m��n�����ڵڶ��������Ľ�ƽ����l�ĶԳƵ�P�������Ϊ ��
��3���������ع㣺
����֪����C��6��0����D��2��4��������ֱ��l��ȷ��һ��P��ʹ��P��C��D����ľ���֮����С����ͼ�л�����P��λ�ã�������ͼ�ۼ����������P�����꣮
�������������£������PC+PD����Сֵ��
���𰸡���1����-3��-5������2����-n��-m������3������ͼ��������P��1��-1������![]() .
.
��������
�����������1���۲�ͼ�εó���B��5��3������ֱ��l�ĶԳƵ�B������꼴�ɣ�
��2�������ܽ�õ�һ���Թ��ɣ�д��P��m��n�����ڵڶ��������Ľ�ƽ����l�ĶԳƵ�P������꼴�ɣ�
��3������ͼ������C����ֱ�� l �ĶԳƵ�C�䣬����C��D����l�ڵ�P������CP������ͼ��֪��PC=PC�䣬�����õ�PC+PD=C��D�������ʱP���꼴�ɣ������ù��ɶ������PC+PD����Сֵ���ɣ�
�����������1����������ã�B�䣨-3��-5����
��2����������ã�P�䣨-n��-m����
��3������ͼ������C����ֱ�� l �ĶԳƵ�C�䣬����C��D����l�ڵ�P������CP��
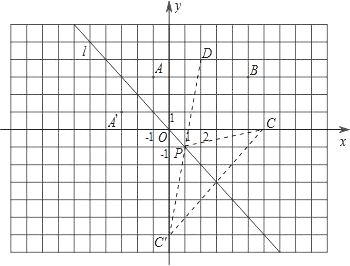
����ͼ��֪��PC=PC�䣬
��PC+PD=PC��+PD=C��D��
����P����
��C��6��0����
��C�䣨0��-6����
��ֱ��C��D�Ľ���ʽΪy=kx-6��
��D��2��4����
��k=5��
��ֱ��C��D�Ľ���ʽΪy=5x-6��
��![]() ��
��![]() ��
��
��P��1��-1����
��PC+PD=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ��4����������ɸ��������dz���ɫ��������ȫ��ͬ��ͨ���������������֣����������Ƶ���ȶ���25%��������ڴ��а��������____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ʋе�Բ����Ƭ�ϣ���AB�Ĵ�ֱƽ���߽���AB�ڵ�C������AB�ڵ�D��
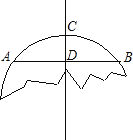
�������˲�Ƭ���ڵ�ԲO����д������������ͼ�ۼ�����
����֪��AB=12cm��ֱ��Ϊ20cm�������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����40Ԫ����5Ԫ/����ij����Ʒ������ʣ���Ǯ��ΪyԪ���������Ʒ����Ϊx������y��x�仯�Ĺ�ϵʽΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֻ�������������У���ÿ�����з�4ֻ������һ�������ɷţ���ÿ�������5ֻ������һ�����ɷţ����ж���ֻ�������ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬����E��EF��AB����BC�ڵ�F��
��1����֤���ı���DBFE��ƽ���ı��Σ�
��2������ABC����ʲô����ʱ���ı���DBFE�����Σ�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A����3��y1����B��0��y2���Ƕ��κ���y=��2��x��1��2+3ͼ���ϵ����㣬��ôy1��y2�Ĵ�С��ϵ��________����y1��y2��y1=y2��y1��y2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��1����x99+x98+x97+��+x+1����ֵ���������������⣬���ǿ�����˼��һ�£��Ӽ��������֣��ȷֱ�������и�ʽ��ֵ��
�٣�x��1����x+1��=x2��1��
�ڣ�x��1����x2+x+1��=x3��1��
�ۣ�x��1����x3+x2+x+1��=x4��1��
��
�ɴ����ǿ��Եõ�����x��1����x99+x98+x97+��+x+1��= ��
������������Ľ��ۣ��������������ļ��㣺
��1������2��50+����2��49+����2��48+��+����2��+1��
��2����x3+x2+x+1=0����x2016��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com