练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

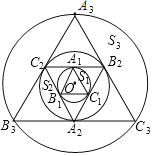
    【题目】如图，小圆O的半径为1，△A1B1C1，△A2B2C2，△A3B3C3，…，△AnBnn依次为同心圆O的内接正三角形和外切正三角形，由弦A1C1和弧A1C1围成的弓形面积记为S1，由弦A2C2和弧A2C2围成的弓形面积记为S2，…，以此下去，由弦Ann和弧Ann围成的弓形面积记为Sn，其中S2020的面积为_____．

    【答案】24036（）

    【解析】

    根据正三角形和圆的关系可依次求出弓形面积，再根据弓形面积寻找规律即可得结论．

    解：∵小圆O的半径为1，△A1B1C1，△A2B2C2，△A3B3C3，…，△AnBnn依次为同心圆O的内接正三角形和外切正三角形，

    ∴S1＝＝，

    S2＝，

    S3＝，

    …

    发现规律：

    Sn＝＝＝（）；

    ∴S2020的面积为：24036（）．

    故答案为：24036（）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，，()，以为直径画圆⊙，点为⊙上一动点．

    （1）判断坐标原点是否在⊙上，并说明理由；

    （2）若点在第一象限，过点作轴，垂足为，连接，且，当时，求线段的长:

    （3）若点是的中点，试问随着的变化点的坐标是否发生变化，若不变，求出点的坐标；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝－x2＋bx＋c与x轴相交于A（－1，0），B（5，0）两点．

    （1）求抛物线的解析式；

    （2）在第二象限内取一点C，作CD垂直x轴于点D，链接AC，且AD＝5，CD＝8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；

    （3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设△ABC，点P是平面内的任意一点（A、B、C三点除外），若点P与点A、B、C中任意两点的连线的夹角为直角时，则称点P为△ABC的一个勾股点．

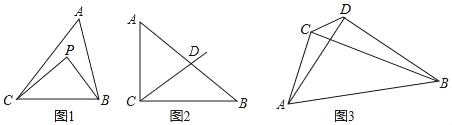
    （1）如图1，若点P是△ABC内一点，∠A＝50°，∠ACP＝10°，∠ABP＝30°，试说明点P是△ABC的一个勾股点．

    （2）如图2，Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，点D是AB的中点，点P在射线CD上，若点P是△ABC的勾股点，则CP＝　 　；

    （3）如图3，四边形ABDC中，DB＝DA，∠BCD＝45°，AC＝，CD＝3．则点D能否是△ABC的勾股点，若能，求出BC的长：若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，⊙O的半径OC垂直于弦AB，垂足为点D，点P在OC的延长线上，连结AP，AC平分∠PAB．

    (1)求证：PA是⊙O的切线；

    (2)若sinP=，AB=16,求⊙O的半径长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

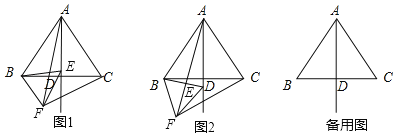
    【题目】已知△ABC是等边三角形，AD⊥BC于点D，点E是直线AD上的动点，将BE绕点B顺时针方向旋转60°得到BF，连接EF、CF、AF．

    （1）如图1，当点E在线段AD上时，猜想∠AFC和∠FAC的数量关系；（直接写出结果）

    （2）如图2，当点E在线段AD的延长线上时，（1）中的结论还成立吗？若成立，请证明你的结论，若不成立，请写出你的结论，并证明你的结论；

    （3）点E在直线AD上运动，当△ACF是等腰直角三角形时，请直接写出∠EBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近日，某中学举办了一次以“弘扬传统文化”为主题的汉字听写比赛，初一和初二两个年级各有600名学生参加，为了更好地了解本次比赛成绩的分布情况，学校分别从两个年级随机抽取了若干名学生的成绩作为样本进行分析，下面是初二年级学生成绩样本的频数分布表和频数分布直方图（不完整，每组分数段中的分数包括最低分，不包括最高分）

    初二学生样本成绩频数分布表

    分组/分

    频数

    频率

    50～60

    2

    60～70

    4

    0.10

    70～80

    0.20

    80～90

    14

    0.35

    90～100

    合计

    40

    1.00

    请根据所给信息，解答下列问题：

    （1）补全成绩频数分布表和频数分布直方图．

    （2）若初二学生成绩样本中80～90分段的具体成绩为：

    80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89

    ①根据上述信息，估计初二学生成绩的中位数为__________．

    ②若初一学生样本成绩的中位数为80，甲同学在比赛中得到了82分，在他所在的年级中位居275名，根据上述信息推断甲同学所在年级为__________（选填“初一”或者“初二”）．

    ③若成绩在85分及以上均为“优秀”，请你根据抽取的样本数据，估计初二年级学生中达到“优秀”的学生人数为__________人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

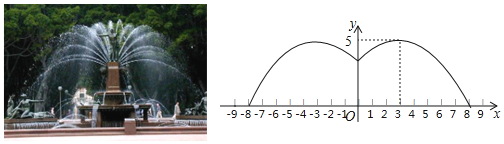
    【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

    （1）求水柱所在抛物线（第一象限部分）的函数表达式；

    （2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

    （3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE＝DF，∠A＝∠D，AB＝DC.

    (1)求证：△AEC≌△DFB；

    (2)若∠EBD＝60°，BE＝BC，求证：四边形BFCE是菱形．

    查看答案和解析>>

    同步练习册答案