
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.
解答 解:∵-8、$\sqrt{16}=4$是整数,
∴它们都是有理数;
∵3.1415926是有限小数,
∴3.1415926是有理数;
∵$\frac{22}{7}=3.\stackrel{•}{1}4285\stackrel{•}{7}$是循环小数,
∴$\frac{22}{7}$是有理数;
∵$\root{3}{9}$,$\sqrt{8}$,1.010010001…,$\frac{π}{3}$都是无限不循环小数,
∴它们都是无理数,
∴无理数有4个:$\root{3}{9}$,$\sqrt{8}$,1.010010001…,$\frac{π}{3}$.
故选:B.
点评 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.


科目:初中数学 来源: 题型:解答题
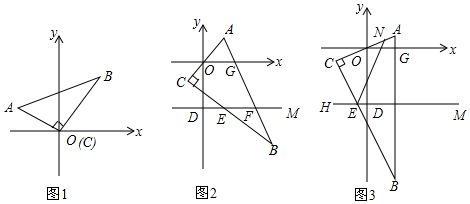
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
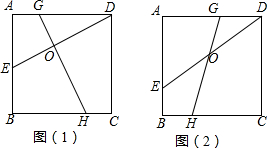
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
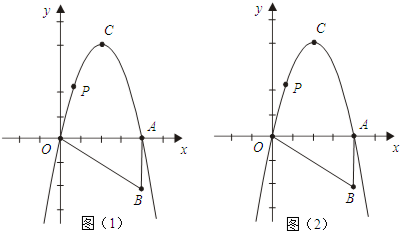
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com