
【题目】如图,在平面直角坐标系中,已知抛物线![]() 过
过![]() ,
,![]() ,
,![]() 三点,点
三点,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,动点
,动点![]() 在抛物线上.
在抛物线上.

![]() ________,
________,![]() ________,点
________,点![]() 的坐标为________;(直接填写结果)
的坐标为________;(直接填写结果)
![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出所有符合条件的点
为直角边的直角三角形?若存在,求出所有符合条件的点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
![]() 过动点
过动点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线.垂足为
轴的垂线.垂足为![]() ,连接
,连接![]() ,当线段
,当线段![]() 的长度最短时,求出点
的长度最短时,求出点![]() 的坐标.
的坐标.
【答案】(1)-2,-3,(-1,0)(2)存在![]() 的坐标是
的坐标是![]() 或
或![]() (3)
(3)![]() 或
或![]()
【解析】
(1)将点A和点C的坐标代入抛物线的解析式可求得b、c的值,然后令y=0可求得点B的坐标;
(2)分别过点C和点A作AC的垂线,将抛物线与P1,P2两点先求得AC的解析式,然后可求得P1C和P2A的解析式,最后再求得P1C和P2A与抛物线的交点坐标即可;
(3)连接OD.先证明四边形OEDF为矩形,从而得到OD=EF,然后根据垂线段最短可求得点D的纵坐标,从而得到点P的纵坐标,然后由抛物线的解析式可求得点P的坐标.
(1)∵将点A和点C的坐标代入抛物线的解析式得:![]() ,解得:b=﹣2,c=﹣3,∴抛物线的解析式为y=x2﹣2x﹣3.
,解得:b=﹣2,c=﹣3,∴抛物线的解析式为y=x2﹣2x﹣3.
∵令x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,∴点B的坐标为(﹣1,0).
故答案为:﹣2;﹣3;(﹣1,0).
(2)存在.理由如下:
如图所示:
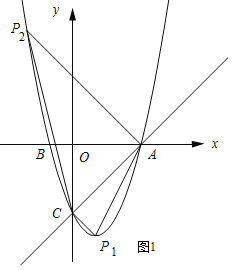
①当∠ACP1=90°.
由(1)可知点A的坐标为(3,0).
设AC的解析式为y=kx﹣3.
∵将点A的坐标代入得:3k﹣3=0,解得:k=1,∴直线AC的解析式为y=x﹣3,∴直线CP1的解析式为y=﹣x﹣3.
∵将y=﹣x﹣3与y=x2﹣2x﹣3联立解得:![]() ,
,![]() (舍去),∴点P1的坐标为(1,﹣4).
(舍去),∴点P1的坐标为(1,﹣4).
②当∠P2AC=90°时.
设AP2的解析式为y=﹣x+b.
∵将x=3,y=0代入得:﹣3+b=0,解得:b=3,∴直线AP2的解析式为y=﹣x+3.
∵将y=﹣x+3与y=x2﹣2x﹣3联立解得:![]() ,
,![]() (舍去),∴点P2的坐标为(﹣2,5).2
(舍去),∴点P2的坐标为(﹣2,5).2
综上所述:P的坐标是(1,﹣4)或(﹣2,5).
(3)如图2所示:连接OD.
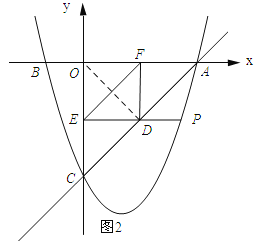
由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短.
由(1)可知.在Rt△AOC中,∵OC=OA=3,OD⊥AC,∴D是AC的中点.
又∵DF∥OC,∴![]() ,∴点P的纵坐标是
,∴点P的纵坐标是![]() ,解得:
,解得:![]() ,∴当EF最短时,点P的坐标是:(
,∴当EF最短时,点P的坐标是:(![]() )或(
)或(![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字2,3,4,5将卡片的背面向上,洗匀后从中任意抽取1 张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号2,3,4的3个小球,这些球除标号外都相同,搅匀后从中任意摸出一个球,将摸到的球的标号作为减数.
(1)用树状图或列表的方法求这两个数的差为0的概率;
(2)如果游戏规则规定:当抽到的这两个数的差为非负数时,则甲获胜;否则,乙获胜,你认为这样的规则公平吗?如果不公平,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为
为![]() 斜边
斜边![]() 上的一点,以
上的一点,以![]() 为半径的
为半径的![]() 与边
与边![]() 交于点
交于点![]() ,与边
,与边![]() 交于点
交于点![]() ,连接
,连接![]() ,且
,且![]() 平分
平分![]() .
.

![]() 试判断
试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个箱子,其中甲箱内有![]() 颗球,分别标记号码
颗球,分别标记号码![]() ,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出
,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出![]() 颗球放入乙箱后,乙箱内球的号码的中位数为
颗球放入乙箱后,乙箱内球的号码的中位数为![]() .若此时甲箱内有
.若此时甲箱内有![]() 颗球的号码小于
颗球的号码小于![]() ,有
,有![]() 颗球的号码大于
颗球的号码大于![]() ,若他们的中位数都为
,若他们的中位数都为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
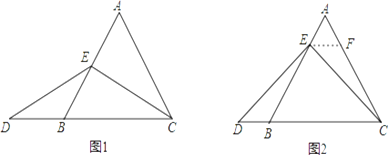
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com